EL TRINOMIO CUADRADO PERFECTO
Para saber si un trinomio es cuadrado perfecto debemos tomar en cuenta lo siguiente:
Para saber si un trinomio es cuadrado perfecto debemos tomar en cuenta lo siguiente:
- verificar si el primer termino y tercer termino son positivos y se pueden extraer las raíces, cuadradas ,
- verificar que el segundo termino sea el doble producto de la primera raíz del primer termino por la raíz del segundo termino
- a continuación si verifico lo anteriormente colocar en un paréntesis las raíces encontradas formando un binomio el signo de separación entre términos puede ser positivo o negativo de acuerdo al signo que tenga el segundo termino y elevarlo al cuadrado y así obtendremos que es igual a elevar un binomio al cuadrado..
Trinomio cuadrado Incompleto
TUTORIA EL SISTEMA DE ECUACIONES DE 2 X 2 METODOS PARA SU REALIZACION
SISTEMAS DE ECUACIONES 2X2 PROBLEMAS
Muchos problemas que requieren la determinación de dos o más cantidades desconocidas pueden ser resueltos por medio de un sistema de ecuaciones lineales. Las cantidades desconocidas se representan con letras, por ejemplo: x, y, etc. y se establece un sistema de ecuaciones que satisfagan las diversas condiciones del problema. La resolución de este sistema conduce a los valores de las incógnitas.
PROBLEMA 1.- El costo total de 5 libros de texto y 4 lapiceros es de $32.00; el costo total de otros 6 libros de texto iguales y 3 lapiceros es de $33.00. Hallar el costo de cada artículo.
PROBLEMA 2. Hallar dos números tales que la suma de sus recíprocos sea 5, y que la diferencia de sus recíprocos sea 1.
PROBLEMA 3. Si a los dos términos de una fracción se añade 3, el valor de la fracción es 1/2 , y si a los dos términos se resta 1, el valor de la fracción es 1/3. Hallar la fracción.
PROBLEMA 4. Se tienen $120.00 en 33 fichas de a $5 y de a $2. ¿Cuántas fichas son de $5 y cuántos de $2?
EL SISTEMA DE ECUACIONES DE 2 X 2 METODOS PARA SU REALIZACION
Método de sustitución
Lo que debemos hacer:
1.- Despejar una de las incógnitas en una de las ecuaciones.
2.- Sustituir la expresión obtenida en la otra ecuación.
3.- Resolver la ecuación resultante.
4.- Calcular la otra incógnita en la ecuación despejada.
Método de reducción o eliminación
Lo que debemos hacer:
1.- Se igualan los coeficientes de una incógnita, salvo el signo, eligiendo un múltiplo común de ambos.
2.- Puede ser el producto de los coeficientes de esa incógnita.
3.- Se suman o restan, según convenga, las ecuaciones.
4.- Se resuelve la ecuación de primer grado resultante.
5.- Se calcula la otra incógnita sustituyendo el valor obtenido en una de las ecuaciones del sistema.
Método de igualación
Lo que debemos hacer:
1.- Se despeja una de las incógnitas en ambas ecuaciones.
2.- Se igualan las expresiones, con lo que obtenemos una ecuación con una incógnita.
3.- Se resuelve la ecuación resultante.
4.- El valor obtenido se sustituye en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita.
5.- Los dos valores obtenidos constituyen la solución del sistema
método gráfico
FUNCIÓN LINEAL..
TUTORIA SISTEMA DE ECUACIONES DE 2 X 2 Y CON DIFERENTES METODOS
METODO DE ELIMINACION
MÉTODO DE SUSTITUCIÓN
MÉTODO DE IGUALACIÓN
MÉTODO GRÁFICO
MÉTODO DE SUMA Y RESTA
TUTORIA DE LA FUNCION LINEAL
EVALUACION DEL SISTEMA DE ECUACIONES DE 2X 2
Escoge la solución correcta de los sistemas de ecuaciones en cada caso:
1.- 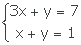
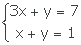
Respuestas:
a)
b)
2.- 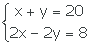
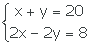
a)
b)
c)
3.- 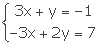
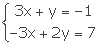
a)
b
c)
4.- 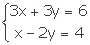
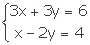
Respuestas:
Asocia a cada uno de estos problemas el sistema de ecuaciones que usarías para resolverlo:
5.- Pedro
compra en una tienda de segunda mano un videojuego de fútbol y dos de
boxeo por 55 dólares. Andrea compra en la misma tienda tres de fútbol y uno de
boxeo por 90 dólares.
Respuestas:
a)
b)
c)
6.- Mercedes y Carlos son hermanos y entre los dos suman 19 años. Sabiendo que la edad de
Mercedes menos uno es igual a la mitad de la edad de Carlos.
Respuestas:
a)
b)
c)
EL SISTEMA INTERNACIONAL DE MEDIDAS (SI). CONVERSIÓN DE UNIDADES
La Radicación.
VIDEOS TUTORIALES.
EJERCICIOS PROPUESTOS:
1. Calcula los valores de las siguientes potencias:
a) 
b)
c)
d)

b)

c)

d)

2. Extraer factores:
a)  =
=
b) =
=
 =
=b)
 =
=3. Introducir factores:
a)  =
=
b) =
=
 =
=b)
 =
=
4. Poner a común índice:


5. Realiza las sumas:
a)  =
=
b) =
=
c) =
=
d) =
=
 =
=b)
 =
=c)
 =
=d)
 =
=
6. Halla las sumas:
a) 
b)
c)
d)

b)

c)

d)

7. Efectúa las sumas:
a)  =
=
b)
 =
=b)

8. Realizar los productos:
a)
 .
.b)
 .
.c)
 .
.
10. Efectúa las divisones de radicales:
a) 
b)
c)

b)

c)

10. Calcula:


11. Opera:

12. Realiza las operaciones con potencias:
a)  .
.
b)
 .
.b)

13. Realiza las operaciones:
a) 
b)
c)
d)

b)

c)

d)

14. Calcula:
a) 
b)

b)

15. Efectuar:
a)  .
.
b) .
.
c)
 .
.b)
 .
.c)

16. Racionalizar los radicales:
a)  .
.
b) .
.
c) .
.
d) .
.
e) .
.
 .
.b)
 .
.c)
 .
.d)
 .
.e)
 .
.17. Racionalizar:
a)  =
=
b) -
-
c) .
.
d) =
=
e)
 =
=b)
 -
-c)
 .
.d)
 =
=e)

NOTACION CIENTÍFICA
CUESTIONARIO DE MATEMÁTICAS PARA DÉCIMO.
1. Extraer factores:
a)  =
=
 =
=
b)  =
=
 =
=2,- Efectúa la división de radicales:

3.- Compruebe la Suma siguiente y diga cual es el procedimiento que siguió :
4.- Realiza el producto:
a)
 .
.b)

5.- Verdadero o Falso . En los espacios en blanco de la tabla ponga una "V" si es verdadero o una"F" si es falso lo siguiente:
Verdadero (V)
|
Falso (F)
| |||
|
| ||||
|
| ||||
|
|
| |||
|
|
| |||
|
|
|
a) La unión de los números .................. y los números irracionales forma el conjunto de los números reales.
b) Todo número racional admite una representación decimal, que es la que se obtiene al dividir el ........................ entre el .............................., por ejemplo 1/2 tiene como expresión decimal 0.5
7..- UNA CON UNA LÍNEA LO CORRECTO:
8.- Con los siguientes datos:
a) ¿Cuantas chicas de 80 EGB practican Futbol?.................................
b) ¿Cuántos chicas juegan Baloncesto?............................
c) ¿Cuántas chicas de 8o EGB y 1o Bachillerato practican atletismo?……………………..
9.- Calcule el área de una circunferencia que tiene un radio de 8,5 cm..
10.- Construya un octógono inscrita en una circunferencia y trace sus diagonales
PROBLEMAS:
11.- Calcule la distancia que ha de recorrer el caminante para llegar al castillo
12.- Con los siguientes datos : A = ( 8 , - 3 ) ; B =( 9 , -2) ; C=( -4. -9) grafique esos puntos en un plano cartesiano
Resolución por el metodo gráfico
Los siguientes videos le ayudarán a resolver algunos de los sistemas propuestos
PRESENTACION DEL DOCENTE TUTOR
Estimados Alumnos
Bienvenidos y en hora buena por haber tomado sus estudios en la Modalidad a Distancia. La competencia profesional es cada día más difícil. Si bien un título por sí solo no tiene significado si no está respaldado por conocimientos sólidos, en mayor desventaja aún se encuentra quien no tiene ni título ni conocimientos.
Usted sabe que el camino por recorrer no es fácil. En una maratón, miles son los que se inscriben y arrancan con el pito de partida; sin embargo apenas unos pocos son los que llegan a la meta.
Recuerde la canción: “También me dijo un arriero
que no hay que llegar primero
si no que hay que saber llegar”.
Que las dificultades no le rindan sino, por el contrario, que le den más coraje para seguir adelante con mayor ahínco.
Su amigo
TUTOR DE LA ASIGNATURA DE MATEMÁTICAS
OBJETIVOS EDUCATIVOS DEL AÑO
- Reconocer una función lineal por mdeio del análisis de su tabla de valores, gráfico o ecuación y conociendo uno de los tres modelos anteriores, determinar los otros dos para comprender y predecir variaciones constantes.
- Aplicar el patrón de la función lineal y sus valores relevantes en la resolución de problemas de la vida cotidiana.
- Contrastar la función lineal con la función exponencial para comprender las diferencias entre variaciones constantes y variables
- Representar y resolver un sistema de dos ecuaciones lineales con dos incógnitas a través de gráficos y algebraicamente para aplicarlos en la solución de situaciones concretas.
- Aplicar el Teorema de Pitágoras para deducir y entender las funciones trigonométricas y las fórmulas usadas en el cálculo de perímetros,áreas, volúmenes, ángulos de cuerpos y figuras geométricas con el propósito de alcanzar un mejor entendimiento de su entorno.
- Realizar conversiones con unidades de medidas del SI y con otros sistemas a través de la comparación y del cálculo, para comprender las equivalencias con unidades usadas comúnmente en nuestro medio-
- Recolectar, representar y analizar datos estadísticos y situaciones probabilísticas relacionadas con lugares históricos, turísticos y bienes naturales, para fomentar y fortalecer la apropiación y cuidado de los bienes culturales y patrimoniales del Ecuador.
Contenidos para la tutoría de Matemáticas para Décimo Año de Educación Básica
BLOQUE DE RELACIONES Y FUNCIONES
- Función lineal
- Patrón creciente o decreciente
- Tabla de valores
- Gráfica
- Ecuación
- Función Exponencial
- Patrón generador
- Tendencia creciente o decreciente
- Sistema de dos ecuaciones lineales con dos incognitas
- Representación gráfica
- Resoluciones algebraicas
- Polinomios
- Operaciones con números reales
BLOQUE NUMÉRICO
- Notación científica
- Expresión decimal con exponentes positivos y negativos
- Expresiones Algebraicas y numéricas
- Simplificación
- Racionalización
- Números Reales
- Resolución con operaciones combinadas de adición, sustracción, multiplicación, división, potenciación y radicación
- Exponentes fraccionarios
BLOQUE DE GEOMETRÍA
- Teorema de Pitágoras
- Aplicaciones en áreas y volúmenes
- Resolución de Problemas
- Pirámides y conos
- Volumen
- Áreas laterales
- Razones Trigonométricas
- Definición
- Aplicación a la resolución de tríangulos rectángulos
- Resolución de problemas
- Ángulos
- Internos en polígonos regulares
- Complementarios, suplementarios , coterminales y de referencia.
BLOQUE DE MEDIDA
- Ángulos notables
- Medidas en radianes en los cuatro cuadrantes
- Conversiones de ángulos entre radianes y grados
- Conversiones
- Entre unidades del sistema internacional de medidas
- Otros sistemas
BLOQUE DE ESTADÍSTICA Y PROBABILIDAD
- Media aritmética
- Cálculo
- Resolución de Problemas
- Probabilidades Simples
- Cálculo
- Representaciones Gráficas
Para poder continuar con los objetivos tratados para décimo año de Educación Básica tenemos que hacer un breve resumen de los números Reales



Cuestionario para la evalucion del segundo quimestre.
 En este ejercicio no tenemos valores de los tres lados, falta uno de los catetos y para calcularlo utilice el Teorema de Pitágoras.
En este ejercicio no tenemos valores de los tres lados, falta uno de los catetos y para calcularlo utilice el Teorema de Pitágoras.
1.- Realizar las siguientes operaciones con potencias:
(−2)2 · (−2)3 · (−2)4 =
2.- Escriba una V (verdadero) o la F (falso) en el casillero de la derecha de las siguientes afirmaciones, según corresponda.
1.- 3(4x + 1 ) = 3(4x) + 3(1) = 12x + 3 Propiedad distributiva de la multiplicación
| |
2.- + a = 2a + a = 3a Simplificación de expresiones
| |
3.- Los términos de la potenciación son: Base, exponente y potencia
| |
4.- El coeficiente del siguiente monomio 6b3c5 3 es igual a 18
| |
5.- 7a – 15 = 2a Ecuación de segundo grado con una incógnita
|
3.- Una con una línea lo correcto:
Producto notable
|
Expresión algebraica
|
Nombre
| |||
(a + b)2
|
=
|
a2 + 2ab + b2
|
Diferencia cuarta
| ||
(a + b)3
|
=
|
a3 + 3a2b + 3ab2 + b3
|
Binomio al cubo
| ||
a2 - b2
|
=
|
(a + b) (a - b)
|
Diferencia de cuadrados
| ||
a3 - b3
|
=
|
(a - b) (a2 + b2 + ab)
|
Diferencia de cubos
| ||
a3 + b3
|
=
|
(a + b) (a2 + b2 - ab)
|
Binomio al cuadrado
| ||
a4 - b4
|
=
|
(a + b) (a - b) (a2 + b2)
|
Trinomio al cuadrado
| ||
(a + b + c)2
|
=
|
a2 + b2 + c2 + 2ab + 2ac + 2bc
|
Suma de cubos
|
4.- ENCIERRE EN UN OVALO LA RESPUESTA CORRECTA:
a) Resuelva la ecuación 2 + 3x = 5x - 6
a) X = - 4
b) X = 4
c) X = 2
B) Carlos le dice a un compañero: El doble de mi edad más 3 es igual al triple de mi edad menos 13, ¿Qué edad tiene Carlos?
En este caso la ecuación que se plantea es: 2x + 3 = 3x -13
a) 15 años
b) 20 años
c) 16 años
d) 18 años
5.- PROBLEMAS:- La suma de los ángulos de un triángulo cualquiera es siempre 180°. Sabiendo que un triángulo rectángulo es aquel que tiene un ángulo de 90°. Por tanto, la suma de los dos ángulos agudos de un triángulo rectángulo es: 180o - 90o = 90°. Completa las líneas de puntos siguientes:
• Si un ángulo agudo de un triángulo rectángulo mide 60°, el otro mide ……........
• Si un ángulo agudo de un triángulo rectángulo mide 30°, el otro mide.....................
• Si un ángulo agudo de un triángulo rectángulo mide 45°, el otro mide.....................
7.- GRAFIQUE Dado los siguientes datos represente gráficamente la ecuación X + Y = 7
X
|
Y = 7 - X
|
1
|
6
|
2
|
5
|
5
|
2
|
6.- Resuelva el siguiente sistema de ecuaciones de 2 x 2 por el método de sustitución
a + b = 1
3a + b = 7
| |||
Respuestas:
| |||
|
7.- Asocia a uno de estos problemas el sistema de ecuaciones que usarías para resolverlo:
Mercedes y Carlos son hermanos y entre los dos suman 19 años. Sabiendo que la edad de Mercedes menos uno es igual a la mitad de la edad de Carlos.
8.- Ordene el proceso correcto para la resolución de un sistema de ecuaciones mediante el método gráfico
a) Se representan gráficamente ambas rectas en los ejes coordenados en el plano cartesiano.
b) Se despeja la incógnita y en ambas ecuaciones.
c) Se construye, para cada una de las dos funciones de primer grado obtenidas, la tabla de valores correspondientes.
d) En este último paso hay tres posibilidades:
1. Si ambas rectas se cortan, las coordenadas del punto de corte son los únicos valores de las incógnitas x e y. Sistema compatible determinado.
2. Si ambas rectas son coincidentes, el sistema tiene infinitas soluciones que son las respectivas coordenadas de todos los puntos de esa recta en la que coinciden ambas. Sistema compatible indeterminado.
3. Si ambas rectas son paralelas, el sistema no tiene solución. Sistema incompatible.
Respuestas:
a, b, c, d
|
a, d, c, b
|
c, d, b, a
|
b, c, a, d
|
9.- Calcula las razones trigonométricas del ángulo C del siguiente triángulo
 En este ejercicio no tenemos valores de los tres lados, falta uno de los catetos y para calcularlo utilice el Teorema de Pitágoras.
En este ejercicio no tenemos valores de los tres lados, falta uno de los catetos y para calcularlo utilice el Teorema de Pitágoras.
Lo primero ponerle nombre a los lados con letras minúsculas a los lados que están enfrente del ángulo con la correspondiente letra mayúscula; es decir a = 14 m, b = 8 m y c es el lado que queremos calcular
Aplicando el Teorema de Pitágoras y calculando las razones trigonométricas tenemos:
10.- Considérense los siguientes datos: 3, 8, 3, 3, 2, 8, 5, 8, 6, 2, 6, 4 ,3 ,2 2, 3, 4, 2,8, 10, 8. 4, 10, 6, 2. Se pide:
a) Construya una tabla de frecuencias
b) Calcule la media aritmética y
c) Calcule el porcentaje de frecuencias.
11.- Una con una línea lo correcto.
|
|
Una función cuadrática es una función polinómica de segundo grado que se escribe : f(x) = ax2 + bx + c
| |
|
|
Tabla de valores
| |
|
|
Una función lineal es una función polinómica de primer grado, en un gráfica se representa como una línea recta y se escribe: f(x) = mx + b.
| |
|
|
tipos de funciones:
|











