EL PLANO CARTESIANO
EL PRODUCTO CARTESIANO
Cuestionario de preguntas de Matemáticas para el segundo quimestre
1.- COMPLETE: CON LAS SIGUIENTES PALABRAS (ABREVIADA , MULTIPLICAMOS, PRODUCTO, NÚMERO.) LOS SIGUIENTES CONCEPTOS
a) LA POTENCIACIÓN
EL PRODUCTO CARTESIANO
Cuestionario de preguntas de Matemáticas para el segundo quimestre
1.- COMPLETE: CON LAS SIGUIENTES PALABRAS (ABREVIADA , MULTIPLICAMOS, PRODUCTO, NÚMERO.) LOS SIGUIENTES CONCEPTOS
a) LA POTENCIACIÓN
La potenciación es una forma _________ de escribir un _______ formado por varios factores iguales.
b) BASE
La base de una potencia es el ______ que _____________ por sí mismo.
2.- UNA CON UNA LINEA LO QUE CORRESPONDA
POTENCIAS
|
DEFINICIÓN DE CONCEPTOS
|
|
a0 = 1
|
Un número elevado a 1 es
igual a sí mismo.
|
|
am : a n =
am - n
|
Producto de potencias con
la misma base
|
|
am · a n =
am+n
|
Un número elevado a 0 es
igual a 1.
|
|
a1 = a
|
División de potencias con
la misma base:
|
3.- Ponga una ( V ) si es verdadero o una ( F ) si es falso.
Conceptos
|
V(verdadero)
|
F(Falso)
|
Potencia de una potencia:
Es otra potencia con la misma
base y cuyo exponente es el producto de los exponentes.
(am)n = am · n
(35)3 = 315
|
||
Producto de potencias con el mismo exponente:
Es otra potencia con el mismo
exponente y cuya base es el producto de las
bases.
an · b n = (a · b) n
25 · 45 = 85
|
||
Cociente de potencias con el mismo exponente:
Es otra potencia con el mismo
exponente y cuya base es el cociente de las
bases.
an : bn = (a : b)n
64 : 34 = 24
|
||
Las potencias de exponente par son
siempre positivas.
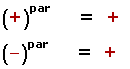
26 = 64
(−2)6 = 64
|
||
Potencias de exponente negativo
La potencia de un número entero con exponente negativo es igual al inverso del número elevado a exponente positivo.
  |
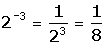4.- Escribe en forma de una sola potencia:
a)
33 · 34 · 3 =
b)
57 : 53 =
c)
(53)4 =
d)
(5 · 2 · 3)4 =
5.- Realizar las siguientes operaciones con potencias:
a)
(−2)2 · (−2)3 · (−2)4
=
b)
(−8) · (−2)2
· (−2)0 (−2) =
c)
(−2)−2
· (−2)3 · (−2)4 =
d)
2−2 ·
2−3 · 24 =
6.- Realiza las siguientes operaciones con potencias:
a)
b)
c)
Bibliografia:
http://www.ditutor.com/numeros_naturales/potenciacion.html
http://www.vitutor.com/di/r/pt_e.html
http://www.vitutor.com/di/r/pt_e.html
TUTORIA INTRODUCCION AL ALGEBRA Y POLINOMIOS
INTRODUCCION
MONOMIOS
Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural.
2x2y3z
Partes de un monomio
1Coeficiente
El coeficiente del monomio es el número que aparece multiplicando a las variables.
2Parte literal
La parte literal está constituida por las letras y sus exponentes.
3Grado
El grado de un monomio es la suma de todos los exponentes de las letras o variables.
El grado de 2x2y3z es: 2 + 3 + 1 = 6
Monomios semejantes
Dos monomios son semejantes cuando tienen la misma parte literal.
2x2y3 z es semejante a 5x2y3 z
SUMA DE MONOMIOSLa suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de los coeficientes.
a) Suma de monomios semejantes: En este caso, los monomios tienen las variables iguales, con los mismos exponentes, procederemos agrupándolos según su parte literal y sumando normalmente:
El truco está en agruparlos debidamente como he hecho en el último ejemplo de arriba. Obviamente, la suma de ambos monomios, será otro monomio semejante.
b) Suma de Monomios no semejantes: A diferencia de antes, los monomios no semejantes no tienen igual parte literal, por lo que procederemos a simplemente anotar esa suma y dejarla planteada: Si los monomios no son semejantes, al sumarlos, se obtiene un polinomio.
La multiplicación de monomios es otro monomio que tiene por coeficiente el producto de los coeficientes y cuya parte literal se obtiene multiplicando las potencias que tengan la misma base, es decir, sumando los exponentes.
axn · bxm = (a · b)xn + m
Para la multiplicación algebraica se mantienen las mismas leyes que para la multiplicación aritmética, las cuales son:
Ley de signos: el resultado es negativo si la cantidad de factores negativos es impar, de lo contrario es positivo.
(+) (+) = +
(-) (-) = +
(+) (-) = -
(-) (+) = -
Ley de exponentes: el producto de dos o más potencias de la misma base es igual a la base elevada a la suma de las potencias.(-) (-) = +
(+) (-) = -
(-) (+) = -
(xm) (xn) = xm + n
Ley conmutativa: el orden de los factores no altera el producto
(x) (z) (y) = (y) (z) (x) = (z) (x) (y) = xyz
Pero en el álgebra se obedece también la ley de los coeficientes.Ley de los coeficientes: el coeficiente del producto de dos o más expresiones algebraicas es igual al producto de los coeficientes de los factores.
(4x) (5y) = 4 · 5 · x · y = 20xy
REGLAS PARA MULTIPLICAR MONOMIOS:
- Se multiplica él termino del multiplicando por él termino del multiplicador.
- Se suman los exponentes de las literales iguales.
- Se escriben las literales diferentes en un solo término resultado.
- Se coloca el signo de acuerdo con las reglas de los signos vistas anteriormente.
Es la división de un monomio entre otro, en fracción se trabaja como reducción de múltiplos iguales.
Pasos a seguir:
Pasos a seguir:
- Se aplica ley de signos
- Se divide el coeficiente del dividendo entre el coeficiente del divisor
- Se aplica ley de los exponentes tomando las letras que no se encuentren como elevadas a cero (nº = 1), y se escriben en orden alfabético.
- Leyes de la división:
Ley de signos: el resultado es negativo si la cantidad de factores negativos es impar, de lo contrario es positivo.
(+) ÷ (+) = +Ley de los cocientes de los coeficientes: el coeficiente del cociente es el cociente de dividir el coeficiente del dividendo entre el coeficiente del divisor.
(-) ÷ (-) = +
(+) ÷ (-) = -
(-) ÷ (+) = -
mx ÷ nxy = (m ÷ n)(x ÷ xy)
Donde m y n son números y n es distinto de cero.
Ley de exponentes: la división de dos o más potencias de la misma base es igual a la base elevada a la diferencia de las potencias.
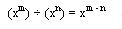
MULTIPLICACION Y DIVISION DE MONOMIOS
1. Halla el valor de:
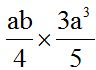Respuesta: 
.
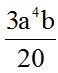Solución:
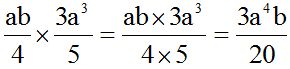
2.- Calcula el producto:
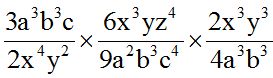
Multiplicamos la parte numérica primero y luego la parte literal sumando los exponentes de las potencias de la misma base:
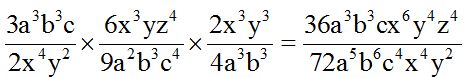
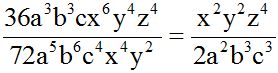
3.- Divide:
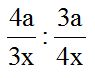Respuesta: 
.
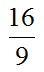Recuerda que para dividir fracciones puedes multiplicar la primera por el inverso de la segunda, es decir, “darle vuelta” a la segunda fracción, que equivale a poner el numerador como denominador y a éste como numerador.
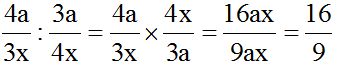4.- Divide:
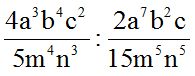Respuesta: 
.
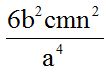BIBLIOGRAFIA
http://www.aulafacil.com/cursos/l10934/ciencia/matematicas/algebra/multiplicacion-algebraica-monomios
http://www.aulafacil.com/cursos/l10684/ciencia/matematicas/operaciones-fracciones-algebraicas/multiplicacion-y-division-de-fracciones-algebraicas
1. Halla el valor de:
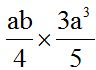Respuesta: .
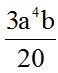Para multiplicar fracciones se halla el producto de numeradores y se
divide por el producto de denominadores. Si se puede, se simplifican
factores comunes:
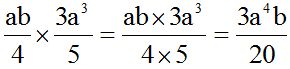
2.- Calcula el producto:
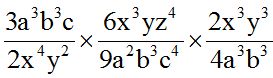
Respuesta: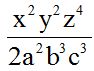 
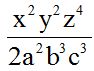
Solución:
Multiplicamos la parte numérica primero y luego la parte literal sumando los exponentes de las potencias de la misma base:
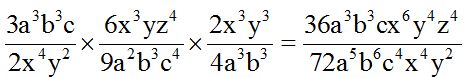
Dividimos la parte numérica primero y luego la parte literal restando
los exponentes de las potencias de igual base y su resultado lo
colocamos donde el exponente era mayor:
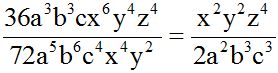
3.- Divide:
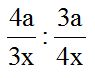Respuesta: .
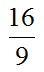Solución:
Recuerda que para dividir fracciones puedes multiplicar la primera por el inverso de la segunda, es decir, “darle vuelta” a la segunda fracción, que equivale a poner el numerador como denominador y a éste como numerador.
También puedes multiplicar el primer numerador por el segundo
denominador y este producto dividir entre el producto del primer
denominador por el numerador de la segunda fracción.
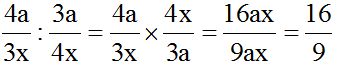
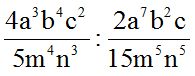Respuesta: 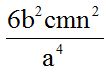.BIBLIOGRAFIA
http://www.aulafacil.com/cursos/l10934/ciencia/matematicas/algebra/multiplicacion-algebraica-monomios
http://www.aulafacil.com/cursos/l10684/ciencia/matematicas/operaciones-fracciones-algebraicas/multiplicacion-y-division-de-fracciones-algebraicas
TUTORIA POTENCIAS Y RAICES
QUE ESUNA POTENCIA
EJERCICIOS MODELO
POTENCIAS FRACCIONARIAS
POTENCIAS CON EXPONENTE NEGATIVO
POTENCIAS NEGATIVAS Y EXPONENTE PAR E IMPAR
LA RADICACION
¿COMO ENCONTRAR RAICES?
EJERCICIOS CON RAICES
POTENCIACION Y RADICACION
QUE ESUNA POTENCIA
EJERCICIOS MODELO
POTENCIAS FRACCIONARIAS
FRACCIONES EXPONENTE CERO
LA RADICACION
¿COMO ENCONTRAR RAICES?
PROPIEDADES DE LAS RAICES
POTENCIACION Y RADICACION
TUTORIA PERÍMETROS, ÁREAS Y VOLÚMENES . POLÍGONOS REGULARES
CONSTRUCCIÓN DE POLÍGONOS INSCRITOS EN UNA CIRCUNFERENCIA
MÉTODO GENERAL.
CONSTRUCCIÓN DE UN EXAGONO.
CONSTRUCCION DE UN PENTAGONO
CONSTRUCCIÓN DE UN TRIANGULO ISÓSCELES
CALCULO DE DIAGONALES QUE TIENE UN POLÍGONO REGULAR
TRAZADO DE DIAGONALES EN LOS POLÍGONOS REGULARES
PRESENTACION DEL DOCENTE TUTOR
Estimados Alumnos
Bienvenidos y en hora buena por haber tomado sus estudios en
la Modalidad
a Distancia. La competencia profesional es cada día más difícil. Si bien obtener un título de Bachiller por sí solo no tiene significado si no está respaldado por conocimientos
sólidos, en mayor desventaja aún se encuentra quien no tiene ni título ni
conocimientos.
Trate desde ahora, con toda decisión, de ser de los que llegan y no solo
de los que arrancan.
Puede haber y de hecho habrá dificultades en el camino, incluso caídas.
Esto es normal a lo largo de nuestras vidas, pero piense que lo importante no es no caer sino siempre
saber levantarse y seguir adelante.
Recuerde la canción:
“También me dijo un
arriero
que
no hay que llegar primero
si no
que hay que saber llegar”.
El sacrificio de ahora es la simiente que fructificará en el triunfo de mañana, con el riego diario del esfuerzo.
De usted depende. . . . . . . . . . . . . . ¡adelante!
Su amigo
Marco Cevallos
TUTOR DE LA ASIGNATURA DE MATEMÁTICAS
TUTOR DE LA ASIGNATURA DE MATEMÁTICAS
OBJETIVOS EDUCATIVOS DEL AÑO:
- Reconocer las variables como elementos necesarios de la Matemática, mediante la generalización de situaciones para expresar enunciados simples en lenguaje matemático.
- Operar con números enteros, a través de la aplicación de las reglas y propiedades de las operaciones en el conjunto Z, con los racionales fraccionarios y decimales positivos para aplicarlos en la resolución de problemas.
- Aplicar conceptos de proporcionalidad a través del cálculo de perímetros, áreas y volúmenes de figuras y de cuerpos (prismas y cilindros) semejantes para resolver problemas.
- Reconocer las diferentes líneas particulares de un triángulo, mediante representaciones gráficas y la aplicación de sus propiedades en la resolución de problemas.
- Analizar, comprender, representar y expresar informaciones nacionales en diversos diagramas mediante el cálculo de frecuencias absolutas y acumuladas, para fomentar y fortalecer la apropiación de los bienes del país.
EJE CURRICULAR: Desarrollar el pensamiento lógico y crítico para interpretar y resolver problemas de la vida.
EJE DE APRENDIZAJE: El razonamiento, la demostración, la comunicación, las conexiones y/o la representación
1. RELACIÓN ENTRE COMPONENTES CURRICULARES
FECHA
|
CONTENIDOS
|
DESTREZAS CON CRITERIOS DE DESEMPEÑO
|
ESTRATEGIAS METODOLÓGICAS/ACTIVIDADES
| |||||
PRIMER QUIMESTRE
| ||||||||
Conjunto de números enteros.
| ||||||||
15/09/2012
|
Representación en la recta numérica. Valor absoluto. Ordenación
|
Leer y escribir números enteros, racionales fraccionarios y decimales positivos.
Ubicar números enteros, racionales fraccionarios y decimales positivos en la recta numérica.
Ordenar y comparar números enteros, racionales fraccionarios y decimales positivos.
|
Realizar un mapa conceptual sobre los números enteros. Concepto, ordenación, ubicación en la recta numérica.
Realizar ejer. 4, 6 pág.11. Ejer. 8, 9 pág. 12.
| |||||
22/09/2012
|
. Adición y Sustracción
Sucesiones con adiciones y sustracciones
|
Resolver las cuatro operaciones de forma independiente con números enteros, racionales fraccionarios y decimales positivos.
Generar sucesiones con números enteros.
| ||||||
29/09/2012
|
. Multiplicación y División
|
Resolver las cuatro operaciones de forma independiente con números enteros, racionales fraccionarios y decimales positivos.
| ||||||
6 /10/2012
|
Potenciación y Radicación
Operaciones combinadas con números enteros.
|
Resolver las cuatro operaciones de forma independiente con números enteros, racionales fraccionarios y decimales positivos.
• Resolver operaciones combinadas de adición, sustracción, multiplicación y división exacta con números enteros, racionales fraccionarios y decimales positivos.
|
Realizar un cuadro sinóptico de las propiedades de la potenciación, con ejemplos generados.
Realizar el ejercicio 46, 55, 60, 61, 63,73,75 pag. 31.
| |||||
13 /10/2012
|
Evaluación del bloque
| |||||||
NUMEROS FRACCIONARIOS
| ||||||||
20/10/2012
|
Concepto, comparación, fracción de un número.
|
Leer y escribir números enteros, racionales fraccionarios y decimales positivos.
Ubicar números enteros, racionales fraccionarios y decimales positivos en la recta numérica.
| ||||||
27/10/2012
|
Fracciones equivalentes
|
Ordenar y comparar números enteros, racionales fraccionarios y decimales positivos.
|
Realizar ejer. 7,8,9, 14, 15 pagina . 40,41
| |||||
10 /11/2012
|
Adición y sustracción
|
Resolver las cuatro operaciones de forma independiente con números enteros, racionales fraccionarios y decimales positivos.
| ||||||
17 /11/2012
|
Multiplicación y División. Potenciación, Radicación
|
Resolver las cuatro operaciones de forma independiente con números enteros, racionales fraccionarios y decimales positivos.
| ||||||
24 /11/2012
|
Operaciones combinadas.
|
• Resolver operaciones combinadas de adición, sustracción, multiplicación y división exacta con números enteros, racionales fraccionarios y decimales positivos.
|
Resolver ejercicio 46, 47, pagina 51. El ejercicio 52, 53 pagina 55.
| |||||
24 /11/2012
|
Evaluación del bloque
|
En una cartulina dibujar un Tamgram de las dimensiones 20 x 20, para trabajar en clase.
| ||||||
NUMEROS DECIMALES
|
Volúmenes de Prismas
| |||||||
1 /12/2012
|
Lectura, representación, orden
|
Leer y escribir números enteros, racionales fraccionarios y decimales positivos.
Ubicar números enteros, racionales fraccionarios y decimales positivos en la recta numérica.
Ordenar y comparar números enteros, racionales fraccionarios y decimales positivos.
|
Lectura de las páginas 68-69-70.
Realizar un cuadro sinóptico del conjunto de números racionales.
| |||||
8 /12/2012
|
Operaciones con decimales
|
Resolver las cuatro operaciones de forma independiente con números enteros, racionales fraccionarios y decimales positivos.
| ||||||
1 5/12/2012
|
Sucesiones con operaciones combinadas
|
• Resolver operaciones combinadas de adición, sustracción, multiplicación y división exacta con números enteros, racionales fraccionarios y decimales positivos.
|
Generar dos problemas de la vida cotidiana con números decimales aplicando las cuatro operaciones básicas.
| |||||
22 /12/2012
|
Volúmenes de poliedros
|
• Deducir y aplicar las fórmulas para el cálculo del volumen de prismas y de cilindros.
| ||||||
29 /12/2012
|
Volúmenes de cuerpos de revolución.
|
• Deducir y aplicar las fórmulas para el cálculo del volumen de prismas y de cilindros.
|
Lectura de la pag. 84, 85, 86.
Realizar ejercicios 51, 55, 59
| |||||
5 /01/2013
|
Evaluación del bloque
|
Llevar a la clase una regla y figuras geométricas para calcular los volúmenes.
| ||||||
SEGUNDO QUIMESTRE
| ||||||||
POLIGONOS, TRIANGULOS, CUADRILATEROS
| ||||||||
2/02/2013
|
Polígonos
|
Conocer los conceptos geométricos elementales y aplicarlos en problemas de la vida cotidiana.
|
Lectura de las páginas 101, 102,103.
| |||||
09/02/2013
|
Triángulos y cuadriláteros
|
Definir y representar medianas, mediatrices, alturas ybisectrices
de un triángulo en gráficos.
Determinar el baricentro, ortocentro, incentro y circuncentro de un
triángulo en gráficos.
|
Realizar un regla T de las diferencias y semejanzas de los cuadriláteros y triángulos.
| |||||
16/02/2013
|
Expresiones algebraicas
|
Expresar un enunciado simple en lenguaje matemático
|
Realizar el ejercicio 50, 51, 53 pagina 118.
| |||||
23/02/2013
|
Operaciones con expresiones algebraicas
(Adición y sustracción)
|
Reconocer y agrupar monomios homogéneos..
| ||||||
02/03/2013
|
Operaciones con expresiones algebraicas
(Multiplicación)
|
Reconocer y agrupar monomios homogéneos..
|
Ingresa a la plataforma virtual del colegio, y descarga los ejercicios que el tutor envía
| |||||
09/03/2013
|
Repaso del bloque
| |||||||
16/03/2913
|
Evaluación del bloque
| |||||||
PROPORCIONALIDAD GEOMETRICA
| ||||||||
23/03/2013
|
Teorema de Tales
|
Aplicar el teorema de Thales en la resolución de figuras geométricas similares.
|
Realizar el ejercicio 4, 5, página 143.
| |||||
06/04/2013
|
Triangulo en posición de Tales
|
Determinar la escala entre figuras semejantes con la aplicación de
Thales.
| ||||||
13/04/2013
|
Aplicaciones del Teorema de Tales
|
Aplicar el teorema de Thales en la resolución de figuras geométricas similares.
|
Basándose en el ejercicio resuelto de la página 165, resuelve los problemas 92, 93 página 170.
| |||||
20/04/2013
|
Triángulos semejantes
|
Reconocer la semejanza de triángulos en la resolución de problemas.
| ||||||
27/04/2013
|
Evaluación del bloque
| |||||||
TABLAS Y GRAFICOS
| ||||||||
04/05/2013
|
Graficas cartesianas
|
Reconocer los pares ordenados con enteros y ubicar en el plano cartesiano
|
Graficar en el plano cartesiano una figura geométrica, e indica los pares ordenados de sus vértices.
| |||||
11/05/2013
|
Estudios estadísticos
|
Recoger, analizar, organizar y representar, datos estadísticos relativos a los diferentes ámbitos de la vida cotidiana.
| ||||||
18/05/2013
|
Tablas y gráficos estadísticos.
|
Calcular y contrastar frecuencias absolutas y acumuladas de una
serie de datos gráficos.
|
En el receso formar grupos de 4 compañeros, y realizar una encuesta sobre los materiales más frecuentes de reciclaje. Organice su información, calcule la Moda, La Mediana, y la Desviación estandar
| |||||
Cuestionario de Matemáticas para Octavos Educación Básica
1.- Escriba una V (verdadero) o la F (falso) en el casillero de la derecha de las siguientes afirmaciones, según corresponda.
1.- Un numero entero es aquel que tiene números positivos, números negativo y el cero
| |
2.- Una fracción es propia cuando el numerador es mayor que el denominador
| |
3.- Los términos de la potenciación son: Base, exponente y potencia
| |
4.- La suma de los ángulos de un triángulo suman 180 grados
| |
5.- 9 > 7 y 5 < 4 entonces 4+1 = 5
| |
6.- La raíz cuadrada de 81 es igual a 8
| |
7.- Una fracción es compleja cuando en el numerador tiene una operación indicada y en el denominador puede tener una fracción
| |
8.- Para sumar el perímetro de un cuadrado se suman los cuatro lados es decir:
Pc = L1+L2+L3+L4
| |
9.- Cuando se suman dos números se obtiene una resultado total por ejemplo:
3 + 5 = 8 -2 +(-2) = -4 5 + 0 = 5
| |
10.- Un exponente es un número que indica cuantas veces, el numero base se utiliza como factor. Por ejemplo 32 = 3 x 3 = 9
|
2.- En el paréntesis ubicado a la izquierda de las premisas, escriba las letras que corresponda a la respuesta correcta de entre las opciones de la derecha.
Premisas
|
Respuestas
|
1. ( ) 53 = 125
2. ( ) 5 –2 = 3
3. ( ) 7 + 3 – (- 4)= 14
4. ( ) -1
5. ( ) Raíz de 81=9
6. ( ) ¼
7. ( ) 0.65
|
(A) Resta
(B) Suma de enteros combinados
(C) Potencia
(D) Fracción
(E) Numero entero
(F) Raíz
(G) Numero decimal
|
3.- A continuación se presentan cuatro preguntas; razone y escriba la respuesta (solo una) en el espacio en blanco de la derecha, con las opciones que se dan a continuación: NÚMEROS ENTEROS; FRACCIÓN PROPIA; NUMERO MIXTO; TRIANGULO.
1.- ¿Cómo se llama el cuerpo geométrico que tiene tres lados?
| |
2.- Cuando el numerador es menor que el denominador; ¿Cómo se llama a la fracción?
| |
3.- ¿Cómo se llama al número que tiene un número entero y una fracción?
| |
4.- Cuando existen los siguientes números +3; -3; 0 ¿Cómo se llaman a esos números?
|
ENCIERRE EN UN OVALO LA RESPUESTA CORRECTA:
4.- ¿Cuál es el Orden descendente de los siguientes números enteros:
+2; + 4; – 6; + 8; – 10; + 12; 0; + 14 ?
a) 14; + 12; - 10; +8; - 6; + 4; + 2 ; 0
b) 0; +2; +4; -6; +8; -10; +12; +14
c) +14; +12; +8; +4; +2; 0; -6; -10
5.- En el siguiente número decimal: 74,326547 ¿cuantas cifras decimales tiene?
a) Una cifra decimal
b) Dos cifras decimales
c ) Seis cifras decimales
d) ninguna cifra decimal
6.- Cuando utilizamos un termómetro; hacemos una referencia a un ejemplo de:
a) números fraccionarios
b) números decimales
c) números enteros
7.- ¿Cuántos grados tiene el tercer ángulo de un triángulo cuyos otros ángulos son 40 grados y 65 grados?
a) 65 grados
b) 60 grados
c) 75 grados
d) 90 grados
PROBLEMAS:
8.- En un día de trabajo (8 horas), un obrero ha hecho 15 cajas ¿Cuántos días de trabajo tardará en hacer 90 cajas?
a) 5 días
b) 6 días
c) 3 días
d) 2 días
9.- La suma de dos artefactos eléctricos es de $187,96; si uno de los artefactos eléctricos costo $ 45,60 ¿Cuánto vale el otro?
a) $ 233,56
b) $ 142,36
c) $ 142,90
d) $ 142.96
10.- En una encuesta realizada con los alumnos de octavo de Educación Básica del Colegio a Distancia “Don Bosco” para saber cuántos hijos se ha obtenido los siguientes resultados: 2; 3; 1; 2; 3; 2; 5; 4; 2; 3; 1; 4; 2; 3; 6; 2; 1 ;3. Complete la tabla con la frecuencia que se repiten los datos y grafique los resultados obtenidos.
Números
|
frecuencia
|
1
| |
2
| |
3
| |
4
| |
5
| |
6
|
(y)
| |||||||||
 | |||||||||
 0 |
(x)
| ||||||||
Módulo 1
Bloque numérico
Objetivo:
Reconocer el uso de los números enteros negativos en situaciones cotidianas, mediante la interacción con su entorno y de hechos concretos.
Bloque de relaciones y funciones
Objetivo:
Representar las figuras geométricas mediante el uso del material concreto siguiendo pautas específicas para resolver problemas.
Bloque geométrico
Objetivo:
Definir analíticamente y gráficamente lo que es un par ordenado para representarlo en el plano cartesiano.
Módulo 2
Bloque numérico
Objetivo:
Operar con números enteros, a través de la aplicación de las reglas y propiedades de las operaciones con el conjunto Z y aplicarlas en la resolución de problemas.
Bloque de estadística y probabilidad
Objetivo:
Analizar, comprender, representar y expresar informaciones nacionales en diferentes diagramas mediante el cálculo de frecuencias absolutas y acumuladas, para fomentar y fortalecer la apropiación de los bienes del país.
Bloque geométrico
Objetivo:
Reconocer la congruencia de triángulos en la resolución de los problemas.
Módulo 3
Bloque numérico
Objetivo:
Operar con números enteros, a través de la aplicación de las reglas y propiedades de las operaciones con el conjunto Z y aplicarlas en la resolución de problemas.
Bloque de relaciones y funciones
Objetivo:
Reconocer las variables como elementos necesarios de la Matemática, mediante la generalización de situaciones para expresar enunciados simples en lenguaje matemático.
Bloque geométrico
Objetivo:
Reconocer las diferentes líneas particulares de un triángulo, mediante representaciones gráficas y la aplicación de sus propiedades en la resolución de problemas.
Módulo 4
Bloque numérico
Objetivo:
Operar con números enteros y fracciones, a través de la aplicación de las reglas y propiedades de la radicación y potenciación, para aplicarlos en la resolución de problemas.
Bloque de relaciones y funciones
Objetivo:
Reconocer las variables como elementos necesarios de la Matemática, para expresar enunciados simples como monomios y operaciones con monomios.
Módulo 5
Bloque numérico
Objetivo:
Operar con números enteros, a través de la aplicación de las reglas y propiedades de las operaciones con el conjunto Z y aplicarlas en la resolución de problemas.
Bloque de medida
Objetivo:
Aplicar conceptos de proporcionalidad a través del cálculo de perímetros, áreas y volúmenes de figuras y de cuerpos (prisma y cilindros) semejantes para resolver problemas.
Bloque geométrico
Objetivo:
Reconocer las diferentes líneas particulares de un triángulo, mediante representaciones gráficas y la aplicación de sus propiedades en la resolución de problemas acerca de semejanzas de triángulos.
Módulo 6
Bloque numérico
Objetivo:
Operar con números enteros, a través de la aplicación de las reglas y propiedades de las operaciones con el conjunto Z, con los racionales fraccionarios y decimales positivos para aplicarlos en la resolución de problemas.
Bloque geométrico
Objetivo:
Aplicar conceptos de proporcionalidad a través del cálculo de volúmenes de figuras y de cuerpos regulares (prismas y cilindros) semejantes para resolver problemas.
ÍNDICE
Módulo 1: La Tierra: un planeta con vida
Bloque numérico:
* Los números enteros
* Los números enteros en la recta numérica
* Relación de orden con los enteros
Bloque de Relaciones y Funciones:
El plano cartesiano
* Sistema cartesiano de coordenadas
* Puntos sobre los ejes
Bloque geométrico:
* Construcción de figuras geométricas : triángulos, cuadriláteros, pentágonos, hexágonos
* Banco de ejercicios y problemas
* Evaluación sumativa
Proyecto 1: Zoom a nuestro planeta
MatemáticaMENTE
Autoevaluación
Módulo 2: La naturaleza y sus cambios
Bloque numérico:
Suma y resta de números enteros
* Propiedades de la suma de enteros
Bloque de Estadísticas y Probabilidad:
Cálculo y análisis de frecuencias absoluta
Cálculo y análisis de frecuencia absoluta acumulada
* Proceso para hallar las frecuencias absolutas acumuladas
Representación gráfica, análisis e interpretación
* Tipos de gráficos estadísticos
* Construcción de los gráficos estadísticos en Excel
Bloque Geométrico:
Congruencia de triángulos
Congruencia de figuras planas
* Banco de ejercicios y problemas
* Evaluación sumativa
Proyecto 2: Estadística de mi país
* MatemáticaMENTE
* Autoevaluación
Módulo 3: Un buen clima en la naturaleza y en el trabajo
Bloque Numérico:
Multiplicación y división con los números enteros
* Multiplicación de números enteros
* División de números enteros
* Propiedades de la multiplicación
Bloque de Relaciones y Funciones:
Sucesiones con enteros
* Sucesión aritmética
Bloque de geométrico:
Líneas y puntos notables de los triángulos
* Banco de ejercicios y problemas
* Evaluación sumativa
Proyecto 3: Ábaco casero
* MatemáticaMENTE
* Autoevaluación
Módulo 4: El universo infinito
Bloque Numérico:
La potenciación
La radicación
* Extracción de factores del radical
* Radicales semejantes
Bloque de Relaciones y Funciones:
Monomios
Operaciones con monomios
* Reducción de términos semejantes
* Productos entre monomios
* Cocientes de monomios
* Los signos de agrupación
* Banco de ejercicios y problemas
* Evaluación sumativa
Proyecto 4: Aprendiendo a escribir fórmulas en la computadora
* MatemáticaMENTE
* Autoevaluación
Módulo 5: El agua, un medio de vida
Bloque Numérico:
Jerarquización de operaciones
Bloque de medida:
Proporcionalidad
* Propiedad de las proporciones
* Proporciones directa e inversamente proporcionales
Escalas
* Cálculo de un valor
Teorema de Thales
Bloque Geométrico:
* Semejanzas de triángulo
* Banco de ejercicios y problemas
* Evaluación sumativa
Proyecto 5: Método gráfico para aplicar escalas
* MatemáticaMENTE
* Autoevaluación
Módulo 6: La matemática en la vida diaria
Bloque Numérico:
Los números racionales
* Representación de un número racional
* Orden y comparación
* Operaciones con números racionales
Los números decimales positivos
* Adición y sustracción de números decimales
* Multiplicación de números decimales
* División de números decimales
Uso de la tecnología para el cálculo de operaciones con números enteros
Bloque Geométrico:
* Volumen y capacidad de cuerpos
* Volumen de prismas
* Volumen de cilindros
* Teorema de Thales en el cálculo de áreas y volúmenes
* Banco de ejercicios y problemas
* Evaluación sumativa
Proyecto 6: El genial Arquímides
* MatemáticaMENTE
* Autoevaluación
OPERACIONES CON FRACCIONES
SUMA Y RESTA DE FRACCIONES HOMOGENEAS
FRACCIONES EQUIVALENTES
SUMA DE FRACCIONES HETEROGENEAS
SUMA Y RESTA DE FRACCIONES HETEROGENEAS
RAIZ CUARTA DE UNA FRACCIÓN
SUMA Y RESTA DE NÚMEROS ENTEROS ejemplos básicos para realizar operaciones de suma y resta de números enteros
Polinomio aritmético con signos de Agrupación destrucción de paréntesis, llaves, corchetes, aplicación de la ley de los signos.
MULTIPLICACIÓN DE NÚMEROS ENTEROS Y APLICACIÓN DE LA LEY DE LOS SIGNOS
La División de Números Enteros
LA POTENCIACIÓN
Ejercicios básicos de La Potenciación
La ley de los Exponentes
LA RADICACIÓN
Ejercicios de LA RADICACIÓN
Aplicación de propiedades en la radicación
PROPIEDADES DE LA RADICACIÓN
EL CONJUNTO DE LOS NÚMEROS RACIONALES
Números Fraccionarios y Operaciones con números fraccionarios
Resta de Números Fraccionarios
Representación de fracciones
Representación grafica de una fracción
Fracciones impropias
Operaciones con números fraccionarios
Simplificación de fracción compleja
Multiplicación de números mixtos y fraccionarios
LOS NÚMEROS DECIMALES
Conversión de decimales a fracción
Fracción generatriz
CUESTIONARIO PARA LA EVALUACIÓN PARA OCTAVOS
- Números Racionales
- Números Fraccionarios
- Representación Gráfica de los números decimales
- Suma y resta de fracciones
- MULTIPLICACIÓN DE FRACCIONES
DIVISIÓN DE FRACCIONES
FRACCIONES CON POTENCIAS
- Números Decimales
CUESTIONARIO DE MATEMATICAS PARA OCTAVOS
1.- Escriba una V (verdadero) o la F (falso) en el
casillero de la derecha de las siguientes afirmaciones, según corresponda.
.- La suma de los ángulos de un triángulo suman 180 grados
|
|
.- 9 > 7 y 5 < 4 entonces 4+1 = 5
|
|
.- Para sumar el perímetro de
un cuadrado se suman los cuatro lados es decir:
Pc = L1+L2+L3+L4
|
|
.- Cuando se suman dos números
se obtiene una resultado total por ejemplo:
3 + 5 = 8 -2 +(-2) = -4 5 + 0 = 5
|
|
.- Un exponente es un número
que indica cuantas veces, el numero base se utiliza como factor. Por ejemplo 32 = 3 x 3 = 9
|
ENCIERRE
EN UN OVALO LA RESPUESTA CORRECTA:
2. ¿Cuál es el Orden descendente de los
siguientes números enteros:
+2; + 4; – 6; + 8; – 10; + 12;
0; + 14 ?
a)
14; + 12;
- 10; +8; - 6; + 4; + 2 ; 0
b)
0;
+2; +4; -6; +8; -10; +12; +14
c)
+14; +12; +8; +4; +2; 0; -6; -10
3. En el siguiente número decimal: 74,326547 ¿cuantas cifras decimales
tiene?
a)
Una cifra decimal
b)
Dos cifras decimales
c)
Seis cifras decimales
d)
Ninguna
4.- Calcule el área de una circunferencia que tiene un
radio de 6 cm..
PROBLEMAS:
5.
Calcule la distancia que ha de recorrer el caminante para llegar al castillo
6. Con los
siguientes datos : A = ( 2 , 3 ) ; B =( 5 , -4) ; C=( -5. -2) grafique esos puntos en un plano
cartesiano
7. Construya un pentágono inscrita en una
circunferencia y trace sus diagonales
8. EFECTÚE LA SIGUIENTE OPERACIÓN:
9.- En el paréntesis ubicado a la izquierda de las premisas,
escriba las letras que corresponda a la respuesta correcta de entre las
opciones de la derecha.
Premisas
|
Respuestas
|
|
(A)
Diferencia
(B)
Suma
(C)
Sucesión
(D)
Fracción
(E)
Formula
(F)
Potencia
(G)
Raíz cuadrada
|
CUESTIONARIO DE EXÁMENES DE MATEMÁTICAS PARA OCTAVOS EBG DEL SEGUNDO QUIMESTRE
1.- Escriba una V (verdadero) o la F (falso) en el casillero de la derecha de las siguientes afirmaciones, según corresponda.
1.- Un monomio es aquel que tiene un solo termino
| |
2.- Una fracción es propia cuando el numerador es mayor que el denominador
| |
3.- Los términos de la potenciación son: Base, exponente y potencia
| |
4.- El coeficiente del siguiente monomio 6b3c5 3 es igual a 18
| |
5.- Un binomio es aquel que tiene tres términos
| |
6.- La raíz cuadrada de 64 es igual a 8
| |
7.- Una fracción es compleja cuando en el numerador tiene una operación indicada y en el denominador puede tener una fracción
| |
2.- En el paréntesis ubicado a la izquierda de las premisas, escriba las letras que corresponda a la respuesta correcta de entre las opciones de la derecha.
Premisas
|
Respuestas
|
1. ( ) a
2. ( ) 3a – 2n
3. ( ) m2 + 2mn + n2
4. ( ) -12
5. ( ) raíz cuadrada 81= 9
6. ( ) ¼
7. ( ) 0.65
|
(A) Binomio
(B) Trinomio
(C) Variable
(D) Fracción
(E) Numero entero
(F) Raíz
(G) Numero decimal
|
3.- A continuación se presentan cuatro preguntas; razone y escriba la respuesta (solo una) en el espacio en blanco de la derecha, con las opciones que se dan a continuación: NÚMEROS ENTEROS; FRACCIÓN IMPROPIA; NUMERO MIXTO; TRINOMIO.
1.- ¿Cómo se llama el polinomio que tiene tres términos?
| |
2.- Cuando el numerador es mayor que el denominador; ¿Cómo se llama a la fracción?
| |
3.- ¿Cómo se llama al número que tiene un número entero y una fracción?
| |
4.- Cuando existen los siguientes número +3; -3; 0; ¿Cómo se llaman a esos números?
|
ENCIERRE EN UN CÍRCULO LA RESPUESTA CORRECTA:
4.- Ordene el siguiente polinomio: 2x4 + 4x7 – 6x + 8x3– 10x2 + 12x5 + 14x6
a) 14x6 + 12x5 - 10x2 + 8x3 - 6x + 4x7 + 2x4
b) – 6x – 10x2 + 8x3 + 2x4 +12x5 + 14x6 + 4x7
c) 4x7 + 14x6 +12x5 + 2x4 + 8x3 – 10x2 - 6x
5.- La factorización es un proceso para obtener:
a) Términos
b) Factores
c) Sumandos
d) Diferencias
6.- El binomio 121x2 – y2 es igual a :
a) ( 11x + y ) ( 11x – y )
b) (11x + y ) (11x +y )
c) (11x – y ) (11x – y)
7.- Términos semejantes son los que tienen igual:
a) Signos
b) Exponentes
c) Parte literal
d) Coeficientes numéricos
PROBLEMAS:
8.- En un día de trabajo (8 horas), un obrero ha hecho 15 cajas ¿Cuántos días de trabajo tardará en hacer 45 cajas?
a) 5 días
b) 6 días
c) 3 días
d) 2 días
9.- La suma de dos artefactos eléctricos es de $ 87,96; si uno de los artefactos eléctricos costo $ 45,60 ¿Cuánto vale el otro?
a) $ 133,56
b) $ 42,36
c) $ 42,30
d) $ 40,36
10.- ¿Cuántos grados tiene el tercer ángulo de un triángulo cuyos otros ángulos son 60 grados y 65 grados?
a) 65 grados
b) 60 grados
c) 55 grados
d) 90 grados
11.- Pedro en un día de trabajo (8 horas), ha hecho 15 sillas ¿Cuántos trabajadores incluyendo a Pedro se necesitara para hacer 90 sillas en un solo día?
b) 6 trabajadores
c) 3 trabajadores
d) 5 trabajadores
12.- La suma de dos artefactos eléctricos es de $187,96; si uno de los artefactos eléctricos costo $ 45,60 ¿Cuánto vale el otro?
a) $ 233,56
b) $ 142,36
c) $ 142,90
d) $ 142.96
1.- Escriba una V (verdadero) o la F (falso) en el casillero de la derecha de las siguientes afirmaciones, según corresponda.
1.- 3(4x + 1 ) = 3(4x) + 3(1) = 12x + 3 Propiedad distributiva de la multiplicación
| |
2.-
| |
3.- Los términos de la potenciación son: Base, exponente y potencia
| |
4.- El coeficiente del siguiente monomio 6b3c5 3 es igual a 18
| |
5.- 7a – 15 = 2a Ecuación de segundo grado con una incógnita
|
2.- En el paréntesis ubicado a la izquierda de las premisas, escriba las letras que corresponda a la respuesta correcta de entre las opciones de la derecha.
Premisas
|
Respuestas
|
1. ( ) a
2. ( ) m –n = 3
3. ( ) 2 , 4 , 6 , 8 , 10……
4. ( ) 3x + 2 < 5
5. ( )
6. ( )
7. ( ) 33 = 27
|
(A) Ecuación
(B) Sucesiones
(C) variable
(D) Formula
(E) Inecuación
(F) Raíz Cuadrada
(G) Potencia
|
3.- Una con una línea lo correcto:
a+ b = 2
2a - b = 5
|
Teorema de Pitágoras
|
c =
|
Sistema de ecuaciones de 2 X 2
|
Cuadriláteros
| |
Función trigonométrica
|
ENCIERRE EN UN OVALO LA RESPUESTA CORRECTA:
4.- Resuelva la ecuación 2 + 3x = 5x - 6
a) X = - 4
b) X = 4
c) X = 2
5.- Carlos le dice a un compañero: El doble de mi edad más 3 es igual al triple de mi edad menos 13, ¿Qué edad tiene Carlos?
En este caso la ecuación que se plantea es: 2x + 3 = 3x -13
a) 15 años
b) 20 años
c) 16 años
d) 18 años
PROBLEMAS:
6.- La suma de los ángulos de un triángulo cualquiera es siempre 180°. Sabiendo que un triángulo rectángulo es aquel que tiene un ángulo de 90°. Por tanto, la suma de los dos ángulos agudos de un triángulo rectángulo es: 180o - 90o = 90°. Completa las líneas de puntos siguientes:
• Si un ángulo agudo de un triángulo rectángulo mide 60°, el otro mide ……........
• Si un ángulo agudo de un triángulo rectángulo mide 30°, el otro mide.....................
• Si un ángulo agudo de un triángulo rectángulo mide 45°, el otro mide.....................
GRAFIQUE
7.- Dado los siguientes datos represente gráficamente la ecuación X + Y = 7
X
|
Y = 7 - X
|
1
|
6
|
2
|
5
|
5
|
2
|
