Tutoria Productos Notables
Un
producto es el resultado de multiplicar dos o más números. Los números que se
multiplican se llaman factores o divisores del producto. Se llaman productos notables
(o productos especiales) a ciertos productos que cumplen reglas fijas y cuyo
resultado puede ser escrito por simple inspección, es decir, sin verificar la
multiplicación.
Cuadrado de un binomio
El cuadrado
de la suma de dos números es igual al cuadrado del primer número, más el
doble del producto del primer número multiplicado por el segundo, más el
cuadrado del segundo.
Consideremos
que  . Tendremos que
. Tendremos que  . Por tanto
. Por tanto
POR EJEMPLO:
1.- Desarrollar

rESOLVIÉNDOLO. Tendremos que el cuadrado del
primer número: 
El doble
del producto del primer número por el segundo: 
El
cuadrado del segundo número: 
Así
pues
2.- Desarrollar

El
cuadrado de la diferencia de dos números es igual al cuadrado del primer
número menos el doble del producto del primer número multiplicado por el
segundo, más el cuadrado del segundo número.
Consideremos
que  .
.
Tendremos
que  .
.
Por
tanto
Es
decir:
POR EJEMPLO
1.- Desarrollar

lA Solución:
2.- Desarrollar

lA Solución: 
Resumiendo con los productos notables de una expresión algebraica en el siguiente cuadro
Producto notable
|
Expresión algebraica
|
Nombre
| |
(a + b)2
|
=
|
a2 + 2ab + b2
|
Binomio al cuadrado
|
(a + b)3
|
=
|
a3 + 3a2b + 3ab2 + b3
|
Binomio al cubo
|
a2 - b2
|
=
|
(a + b) (a - b)
|
Diferencia de cuadrados
|
a3 - b3
|
=
|
(a - b) (a2 + b2 + ab)
|
Diferencia de cubos
|
a3 + b3
|
=
|
(a + b) (a2 + b2 - ab)
|
Suma de cubos
|
a4 - b4
|
=
|
(a + b) (a - b) (a2 + b2)
|
Diferencia cuarta
|
(a + b + c)2
|
=
|
a2 + b2 + c2 + 2ab + 2ac + 2bc
|
Trinomio al cuadrado
|
El producto de un binomio
El producto de la suma por la diferencia
El binomio al cubo
Ejercicio productos notables
BIBLIOGRAFÍA:
http://www.eplc.umich.mx/salvadorgs/matematicas1/contenido/CapIII/3_5_1_cuad_bin.htm
CUESTIONARIO DE MATEMÁTICAS PARA NOVENOS
1.- Escriba una V (verdadero) o la F (falso) en el
casillero de la derecha de las siguientes afirmaciones, según corresponda.
.- Un monomio es aquel que tiene un solo termino
|
V/F
|
.- Una fracción es propia cuando el numerador es mayor que el
denominador
|
|
.- Los términos de la potenciación son: Base, exponente y potencia
|
|
.- El coeficiente del siguiente monomio 6ª2b3c5
3 es igual a 15
|
|
.- Una fracción es compleja
cuando en el numerador
tiene una operación indicada y en el denominador
puede tener una fracción
|
|
.- La suma de los ángulos de
un triángulo suman 180 grados
|
2.- EFECTÚE LAS SIGUIENTES OPERACIONES:
ENCIERRE
EN UN OVALO LA RESPUESTA CORRECTA:
3. ¿Cuál es el Orden descendente del
siguiente polinomio:
2x4
+ 4x7 – 6x + 8x3 – 10x2 + 12x5
+ 14x6 ?
a)
14x6 + 12x5
- 10x2 + 8x3 - 6x + 4x7 + 2x4
b)
–
6x – 10x2 + 8x3 + 2x4 +12x5 + 14x6 + 4x7
c)
4x7
+ 14x6 +12x5 + 2x4 + 8x3 – 10x2 - 6x
4. Sume el siguiente monomio: m+ 2m+ 3m + 5m – 7m
6.- UNA CON UNA LÍNEA LO CORRECTO:
a) ¿Cuantas chicas de 80 EGB
practican Atletismo?.................................
b) ¿Cuántos chicos juegan
Baloncesto?............................
c) ¿Cuántas chicas de 8o EGB
y 1o Bachillerato juegan
Futbol?……………………..
7.- Calcule el área de una circunferencia que tiene un
radio de 6 cm..
Formula:
PROBLEMAS:
8.- Calcule la distancia que ha de recorrer el
caminante para llegar al castillo
9.- Con los siguientes datos : A = ( 5 , - 3
) ;
B =( 3 , -2) ; C=( -4. -2)
grafique esos puntos en un plano cartesiano
10.- Construya un pentágono inscrita en una circunferencia y trace sus diagonales
TUTORIA POLÍGONOS REGULARES , PERÍMETROS, ÁREAS Y VOLÚMENES
TRAZO DE POLÍGONOS REGULARES UTILIZANDO UN COMPÁS, UNA REGLA, UN GRADUADOR Y UN LÁPIZ.
TRAZO DE UN ROMBO
TRAZOS DE POLÍGONOS REGULARES
PERÍMETROS Y ÁREAS
TRAZO DE DIAGONALES DE POLÍGONOS REGULARES
1.- Escriba una V (verdadero) o la F (falso) en el
casillero de la derecha de las siguientes afirmaciones, según corresponda.
.- Un monomio es aquel que tiene un solo termino
|
V/F
|
.- Una fracción es propia cuando el numerador es mayor que el
denominador
|
|
.- Los términos de la potenciación son: Base, exponente y potencia
|
|
.- El coeficiente del siguiente monomio 6ª2b3c5
3 es igual a 15
|
|
.- Una fracción es compleja
cuando en el numerador
tiene una operación indicada y en el denominador
puede tener una fracción
|
|
.- La suma de los ángulos de
un triángulo suman 180 grados
|
2.- EFECTÚE LA SIGUIENTE OPERACIÓN:
ENCIERRE
EN UN OVALO LA RESPUESTA CORRECTA:
3. ¿Cuál es el Orden descendente del
siguiente polinomio:
2x4
+ 4x7 – 6x + 8x3 – 10x2 + 12x5
+ 14x6 ?
a)
14x6 + 12x5
- 10x2 + 8x3 - 6x + 4x7 + 2x4
b)
–
6x – 10x2 + 8x3 + 2x4 +12x5 + 14x6 + 4x7
c)
4x7
+ 14x6 +12x5 + 2x4 + 8x3 – 10x2 - 6x
4. Sume el siguiente monomio: m+ 2m+ 3m + 5m – 7m
a)
18m
b)
8m
c)
4m
6.- UNA CON UNA LÍNEA LO CORRECTO:
a+ b = 2
2a - b = 5
|
Teorema de Pitágoras
|
c =
|
Sistema de ecuaciones de 2 X 2
|
Cuadriláteros
|
|
Función trigonométrica
|
6.- Con los siguientes datos:
a) ¿Cuantas chicas de 80 EGB
practican Atletismo?.................................
b) ¿Cuántos chicos juegan
Baloncesto?............................
c) ¿Cuántas chicas de 8o EGB
y 1o Bachillerato juegan
Futbol?……………………..
7.- Calcule el área de una circunferencia que tiene un
radio de 6 cm..
Formula:
PROBLEMAS:
8.- Calcule la distancia que ha de recorrer el
caminante para llegar al castillo
|
A
|
|
C
|
|
30 m
|
|
70 m
|
|
B
|
Formula:
9.- Con los siguientes datos : A = ( 5 , - 3
) ;
B =( 3 , -2) ; C=( -4. -2)
grafique esos puntos en un plano cartesiano
Introducción
Señoras (es), y Señoritas estudiantes, reciban un cordial saludo y mis mejores deseos de éxito en el presente Año Lectivo; sin duda alguna con su esfuerzo, dedicación y disciplina alcanzarán los objetivos deseados.
En la educación a distancia, el principal protagonista es usted, que voluntariamente se hace responsable de su propio aprendizaje, mientras que el docente cumple el rol de orientador, experto de contenidos quien determina el nivel de conocimientos a conocer por parte del alumno de acuerdo al perfil establecido y además es el responsable de la evaluación de los aprendizajes.
La guía y la tutorias virtuales entonces, es el vínculo entre el alumno y el tutor, por ello es muy importante que lea todos los contenidos de la misma, tome en cuenta los objetivos y sugerencias para su elaboración. Las actividades de la guía están diseñadas con el único propósito de lograr que Ud., interiorice todos los conocimientos o al menos la mayor parte de ellos, mediante la lectura, reflexión, análisis, ejercicios y cálculos matemáticos, representaciones gráficas de números; entre otras actividades que le guíen a construir su propio aprendizaje. Recuerde que la guía es su carta de presentación y refleja su personalidad por tanto debe ser elaborada con el mayor esmero posible, demostrando desde ya, su profesionalismo.
OBJETIVOS EDUCATIVOS DEL AÑO:
- Reconocer y aplicar las propiedades conmutativa, asociativa y distributiva, las cuatro operaciones básicas y la potenciación para la simplificación de polinomios a través de la resolución de problemas.
- Factorizar polinomios y desarrollar productos notables para determinar sus raíces a través de material concreto, procesos algebraicos o gráficos.
- Aplicar y demostrar procesos algebraicos por medio de la resolución de ecuaciones de primer grado para desarrollar un razonamiento lógico matemático.
- Aplicar las operaciones básicas, la radicación y la potenciación en la resolución de problemas con números enteros, racionales e irracionales para desarrollar un pensamiento crítico y lógico.
- Resolver problemas de áreas de polígonos regulares e irregulares, de sectores circulares, áreas laterales y de volúmenes de prismas, pirámides y cilindros, y analizar sus soluciones para profundizar y relacionar conocimientos matemáticos.
- Aplicar el teorema de Pitágoras en la resolución de triángulos rectángulos para el cálculo de perímetros y áreas.
- Recolectar, representar y analizar datos estadísticos en diagramas de tallo y hojas, para calcular la media, mediana, moda y rango.
EJE CURRICULAR: Desarrollar el pensamiento lógico y crítico para interpretar y resolver problemas de la vida.
EJE DE APRENDIZAJE: El razonamiento, la demostración, la comunicación, las conexiones y/o la representación.
1.
RELACIÓN
ENTRE COMPONENTES CURRICULARES
|
FECHA
|
CONTENIDOS
|
DESTREZAS CON CRITERIOS DE DESEMPEÑO
|
ESTRATEGIAS METODOLÓGICAS/ACTIVIDADES
|
|||||
PRIMER QUIMESTRE
|
||||||||
(NÚMEROS RACIONALES) MEDIDAS DE
TENDENCIA CENTRAL
|
||||||||
15/09/2012
|
1.- Fracciones Positivas y Negativas
1.1
Fracciones con signo
1.2
fracciones Equivalentes
1.3
Ubicación de fracciones sobre la recta numérica
1.4
Ordenación de fracciones
|
.
Leer y escribir Números racionales de acuerdo con su definición.
-Ubicar
números enteros, racionales fraccionarios y decimales positivos en la recta
numérica.
|
.
Mediante un cuadro sinóptico clasificar los números racionales
.Mediante
una cadena de secuencias expresar las reglas para representar, ordenar y
comparar números racionales.
Resolver
las actividades de la página 12 y 13.
Resolver
las actividades de la página 14 el
numeral 14 y 16. Y de la página 15 el numeral 18
|
|||||
22/09/2012
|
2.- Operaciones con fracciones
2.1
Adición, sustracción, multiplicación y división.
2.2
Operaciones combinadas
2-3
Potencias y raíces cuadradas
|
Resolver operaciones combinadas de
adición, sustracción, multiplicación y división exacta con números enteros,
racionales fraccionarios y decimales positivos.
|
.
-Mediante rueda de atributos expresar las reglas para la simplificación de
expresiones fraccionarias.
-Resolver los ejercicios de las páginas 16
y 17, aplicando los reglas para realizar las operaciones con fracciones y la
relación entre fracciones y decimales
-Resolver las actividad de las páginas 18
y 19, aplicando las leyes de potenciación y radicación
|
|||||
29/09/2012
|
3.- Relación entre las fracciones y los
decimales
3.1
Expresión decimal de una fracción
3.2
Fracción generatriz de un número decimal
3.3
operaciones con decimales.
4. Aproximación redondeo y error
|
.Resolver
operaciones combinadas de adición, sustracción, multiplicación y división
exacta con números enteros, racionales fraccionarios y decimales positivos.
-Representar números racionales en notación decimal y fraccionaria.
-Efectuar
aproximaciones de números decimales y calcula el error cometido.
|
Mediante un mapa
conceptual explique los métodos para calcular la fracción generatriz de un
número decimal.
-Con la aplicación de los conocimientos
adquiridos resuelva la el taller de autoevaluación y coevaluación de la
pagina 46.
|
|||||
6
/10/2012
|
5.- Estadística : Conceptos
generales
5.1 Variables
estadísticas
5.2 Recolección
de datos
6. Presentación de Datos
6.1
Tabla de distribución de frecuencias
6.2 Gráficos
estadísticos
7. Parámetros estadísticos
7.1
Media aritmética
7.2
Moda
7.3
Mediana
|
--Calcular la
media, mediana y moda de un conjunto de datos estadísticos contextualizados
en problemas pertinentes
|
En el
receso formar grupos de 4 compañeros, y realizar una encuesta sobre los
materiales más frecuentes de reciclaje.
Luego organice y represente los datos estadísticos calcule la media
aritmética, la moda y la mediana.
|
|||||
13 /10/2012
|
Evaluación del bloque
|
|||||||
NÚMEROS IRRACIONALES , PERÍMETROS Y ÁREAS
DE POLÍGONOS
|
||||||||
20/10/2012
|
1.- Teorema de Pitágoras
2.- El conjunto de los números irracionales
2.1
Concepto de número irracional
2.2
Representación gráfica de números irracionales
|
§ Utilizar el Teorema
de Pitágoras en la resolución de triángulos rectángulos
-Leer
y escribir números irracionales de acuerdo con su definición
-Representar
gráficamente números irracionales con el uso del Teorema de Pitágoras
|
- Realizar
la actividad de la página 52 los numerales 1, 2, 3, 4 y 5. Y la Actividad de la página 54 el numeral 6.
|
|||||
27/10/2012
|
2.3
Números irracionales. Orden y comparación
2.4
Operaciones con números irracionales. Suma y Resta
2.5
División y multiplicación de números irracionales
2.6
Operaciones
combinadas
entre números irracionales
|
-Leer y escribir números irracionales de
acuerdo con su definición
Ordenar,
comparar y ubicar en la recta numérica números irracionales con el uso de la
escala adecuada.
Resolver
operaciones combinadas de adición sustracción, multiplicación y división
exactas con números irracionales
|
.Elabore
una tabla de valores y represente las operaciones que se pueden efectuar con
los números irracionales
.Con
el reconocimiento de las operaciones de números irracionales resuelva las actividades de la página 59
|
|||||
10
/11/2012
|
3. Perímetro y área de cuadriláteros y
triángulos
3.1
Perímetro y área de paralelogramos
3.2
Perímetro y área de triángulos
3.3
Perímetro y área de trapecios
|
-Aplicar
las fórmulas de áreas de polígonos regulares en la resolución de
problemas
|
Mediante
un mapa conceptual hable sobre los perímetros y áreas.
|
|||||
17
/11/2012
|
4.
Perímetros y área de otros polígonos
4.1
Polígonos regulares
4.2
Polígonos Irregulares
|
Deducir
las fórmulas para el cálculo de áreas de polígonos regulares por la
descomposición en triángulos.
|
Elabore
un tabla de valores para deducir las fórmulas del área de polígonos regulares
|
|||||
24
/11/2012
|
5. Estimación de áreas
5.1
Aplicación al Teorema de Pitágoras
|
•
Utilizar el teorema de Pitágoras en la resolución de triángulos rectángulos.
|
Aplicando
los conocimientos adquiridos resolver la autoevaluación y coevalución de la
página 78
|
|||||
24
/11/2012
|
Evaluación del bloque
|
|||||||
NUMEROS REALES. POLINOMIOS
|
Volúmenes de Prismas
|
|||||||
1/12/2012
|
1.El conjuntos de los números reales
1.1
Ordenación de los números reales
1.2
Intervalo de números reales
1.3
Aproximaciones y errores
1.4
Truncamiento y redondeo
1.5
Errores
|
Simplificar
expresiones de números reales con la aplicación de las operaciones básicas
Resolver
las cuatro operaciones básicas con números reales
Interpretar
y utilizar los números reales en diferentes contextos , eliguiendo la
notación y la aproximación adecuada en cada caso.
Utilizar
las TIC para realizar operaciones con cualquier tipo de expresión numérica.
Desarrollar
estrategias de cálculo mental y de estimación de cálculos con números reales.
Calcular
el error cometido en operaciones con aproximaciones de números reales.
|
Mediante
un mapa conceptual hable del conjunto de los números reales
|
|||||
8
/12/2012
|
2.-Operaciones con números reales
|
Simplificar
polinomios con la aplicación de las operaciones y de sus propiedades.
|
Resuelva
las actividades de las páginas 94 y 95.
|
|||||
1 5/12/2012
|
3. Algebra
3.1
Operaciones con monomios
3.2
Polinomios
3.3
Valor numérico de un polinomio
3.4
Grado de un polinomio
3.5
Polinomios ordenados y reducidos
3.6
Polinomios completos e incompletos
3,7
Representación concreta de polinomios hasta grado 2
|
• Factorizar polinomios y desarrollar productos
notables.
|
.
Mediante la aplicación de las reglas algebraicas resuelve las actividades de
las paginas 95, 97 y 99
|
|||||
22
/12/2012
|
4.Operaciones con polinomios
4.1
Productos notables
4.2
División de polinomios
4.3
Divisibilidad de polinomios
4-5
Teorema del resto
|
•
Factorizar polinomios y desarrollar productos
notables.
·
Simplifica polinomios con la aplicación de las
operaciones básicas y de las propiedades conmutativa, asociativa y
distributiva.
|
-Mediante
un cuadro de valores explique las
propiedades de los productos notables
|
|||||
29
/12/2012
|
5.- Factorización
Repaso del Bloque
|
• Factorizar polinomios y desarrollar productos
notables.
·
Simplifica polinomios con la aplicación de las
operaciones básicas y de las propiedades conmutativa, asociativa y
distributiva.
|
Resuelva el taller
de autoevaluación y coevaluación de la página 110
|
|||||
5
/01/2013
|
Evaluación del bloque
|
|||||||
SEGUNDO QUIMESTRE
|
||||||||
NUMEROS REALES
.PATRONES DE CRECIMIENTO LINEAL
|
||||||||
2/02/2013
|
1.Potencias de base real y exponente entero
|
Simplifica
expresiones de números reales con exponente negativo con la aplicación de las
reglas de potenciación.
|
Mediante
un mapa conceptual indique las operaciones con potencias
|
|||||
09/02/2013
|
2.Simplificación de expresiones con números
reales
|
Simplifica
expresiones de números reales con exponente negativo con la aplicación de las
reglas de potenciación.
|
Mediante
un cuadro de valores cómo se simplifican las expresiones con números reales
|
|||||
16/02/2013
|
3.Sucesiones
3.1
Término general
3.2
Representación gráfica
|
Presentar
de manera clara y ordenada los ejercicios realizados.
Confiar
en tus propias capacidades para efectuar operaciones matemáticas.
|
Mediante un cuadro
sinóptico explique que son las sucesiones
|
|||||
23/02/2013
|
4.Patrones de crecimiento lineal
|
Reconoce patrones de crecimiento lineal en tablas de
valores y gráficos
Graficar
patrones de crecimiento lineal a partir de su tabla de valores
Presentar
de manera clara y ordenada los ejercicios realizados.
|
Resuelva
las actividades propuestas en las páginas 122, 123
.Mediante
una rueda de atributos explique sobre los patrones de crecimiento lineal y
las funciones de primer grado.
|
|||||
02/03/2013
|
5.Función de primer grado
5.1
Función lineal o proporcionalidad directa
|
Confiar
en tus propias capacidades para efectuar operaciones matemáticas.
Usar
la calculadora de forma racional para operar con potencias.
|
Resuelva
las actividades propuestas en las páginas
125 y 127
|
|||||
09/03/2013
|
Repaso del bloque
|
|||||||
16/03/2913
|
Evaluación del bloque
|
|||||||
ECUACIONES E INECUACIONES DE PRIMER GRADO.
DIAGRAMA DE TALLO Y HOJAS
|
||||||||
23/03/2013
|
1.Igualdad y ecuación
2.
Ecuaciones
2.1
Propiedad de ecuaciones
3.Resolución
de ecuaciones
|
Resolver
ecuaciones de primer grado con procesos algebraicos
Resolver
inecuaciones de primer grado con una incógnita con procesos algebraicos.
|
Mediante
una rueda de atributos defina que es una identidad y que es una ecuación
|
|||||
06/04/2013
|
4. método general para la resolución de
ecuaciones
4.1
Ecuaciones con paréntesis
4.2
Ecuaciones con denominadores
4.3
Aplicación a la resolución de problemas
|
Utilizar
el lenguaje algebraico para generalizar propiedades y simbolizar relaciones
en contextos diversos como la vida cotidiana y los ámbitos socio económicos ,
científico y social.
Tener
predisposición para comprobar los resultados obtenidos en la resolución de
problemas
|
Mediante
un mapa conceptual cuales son los métodos generales para resolver una
ecuación
Con la aprendizajes
y conocimientos aprendidos resuelva la
actividad de la página 146, 147 y 148
|
|||||
13/04/2013
|
5.Desigualdades
5.1
Propiedades
6.Inecuaciones
6.1
Conjunto solución
6.2
Inecuaciones equivalentes
6.3
Resolución de inecuaciones de primer grado con una incógnita
6.4
Inecuaciones de primer grado con dos incógnitas
7. Sistema de inecuaciones
|
Utilizar
los símbolos propios de las desigualdades, así como sus principales
características.
|
Con
la aplicación de los conocimientos resuelva las actividades de las páginas
150 y 151
|
|||||
20/04/2013
|
8. Aplicación a la resolución de problemas
9.Diagrama de tallo y de hojas
|
Resolver
problemas de la vida cotidiana utilizando ecuaciones e inecuaciones.
Representar
datos estadísticos en diagramas de tallo y hojas.
|
.- Realice las
actividades de las páginas 169 y
170aplicando el diagrama de tallo y de hojas.
|
|||||
27/04/2013
|
Evaluación del bloque
|
|||||||
LINEAS DE SIMETRÍA.ÁREAS.MEDIDAS EN GRADOS
DE ÁNGULOS NOTABLES
|
||||||||
04/05/2013
|
1.Transformaciones isométricas o
movimientos
1.1
Simetrías
2.Areas
2.1
Áreas de prismas, pirámides y troncos de pirámide
2.2
Área de cilindros , conos y troncos de cono
|
Reconocer
líneas de simetría en figuras geométricas.
Aplicar
traslaciones y simetrías a figuras en el plano en casos sencillos.
Construir
pirámides y conos a partir de patrones en dos dimensiones.
Calcular
áreas laterales de prismas y cilindros en la resolución de problemas.
|
Mediante
un mapa conceptual explique cuáles son los movimientos en el plano.
-Mediante
cuadros sinópticos explique como se miden los ángulos en los cuatro
cuadrantes
|
|||||
11/05/2013
|
3. Medidas en grados de ángulos notables en
los cuatro cuadrantes
3.1 Razones trigonométricas en cada ángulo
|
Reconocer
medidas en grados de ángulos notables en los cuatro cuadrantes con el uso de
instrumental geométrico.
Afrontar
problemas geométricos con confianza en las propias capacidades.
|
-Con
un cuadro de valores cómo obtenemos las razones trigonométricas de cualquier
ángulo.
.Con la aplicación
de los conocimientos de las líneas de simetría , áreas resuelva, la actividades de las página 186 y 189
|
|||||
18/05/2013
|
4. Razones trigonométricas de un ángulo
cualquiera.
|
Reconocer
medidas en grados de ángulos notables en los cuatro cuadrantes con el uso de
instrumental geométrico.
Afrontar
problemas geométricos con confianza en las propias capacidades.
|
Con
la aplicación de los conocimientos adquiridos razones trigonométricas ,
resuelva las actividades de las páginas 192 y 193
|
|||||
25/05/2013
|
Evaluación del bloque
|
|||||||
Representación de un numero racional en notación decimal
Transformación de un decimal finito a fracción
Transformación de un decimal periódico a fracción
·
Ubicación en la recta numérica de los números racionales
·
Orden y comparación de números racionales.
BLOQUE GEOMETRICO
· Figuras geométricas
· Polígonos regulares
· Líneas de simetría
· Área de un polígono regular
· Figuras geométricas
· Polígonos regulares
· Líneas de simetría
· Área de un polígono regular
BLOQUE DE ESTADISTICA
Y PROBABILIDAD: DIAGRAMA DE TALLO Y HOJAS
Banco de ejercicios y problemas
·
Evaluación sumativa
PROYECTO 1
·
Matemáticamente
·
Autoevaluación
MODULO 2: MATEMATICA E
HISTORIA
BLOQUE GEOMETRICO: TEOREMA DE PITAGORAS
BLOQUE NUMERICO: OPERACIONES CON NUMEROS RACIONALES
·
Operaciones combinadas
·
Multiplicación de números racionales
·
Multiplicación de números decimales
·
División de números racionales
·
División de números decimales
·
Potenciación de números racionales
·
Potenciación de números decimales
·
Radicación de números racionales
·
Radicación de números decimales
NUMEROS IRRACIONALES
·
Suma y resta de números irracionales
·
División de números irracionales
·
Potenciación de números irracionales
·
Radicación de números irracionales
·
Racionalización
·
Banco de ejercicios y problemas
·
Evaluación sumativa
PROYECTO2
·
Matemáticamente
·
Autoevaluación
MODULO3: CONOCIENDO OTRAS CULTURAS
BLOQUE GEOMETRIC: RESOLUCIÓN DE PROBLEMAS SOBRE ÁREAS DE
POLÍGONOS
BLOQUE NUMÉRICO:NÚMEROS REALES (R)
·
Números reales (R)
·
Propiedades de la suma de los números reales
·
Propiedades de la multiplicación de los números
reales
·
División de números reales
·
Operaciones combinadas
·
Potenciación y radicación de números reales
BLOQUE DE RELACIONES Y FUNCIONES: POLINOMIOS
·
Algebra elemental
·
Clasificación de las expresiones algebraicas
·
Simplificación de polinomios
·
Método algebraico para simplificar polinomios
·
Banco de ejercicios y problemas
·
Evaluación sumativa
Proyecto3
·
Matemáticamente
·
Autoevaluación
MODULO4: PRESERVAR Y
APRENDER
BLOQUE DE REALACIONES Y FUNCIONES: OPERACIONES CON
POLINOMIOS
·
Valor numérico de una expresión algebraica
·
Supresión de signos de agrupación
·
División sintética
·
Teorema de residuo
·
Teorema del
factor
·
Productos notables
·
Factorización
BLOQUE DE MEDIDA : MEDIDA DE ÁNGULOS
·
Ángulos
BLOQUE GEOMÉTRICO: SÓLIDOS GEOMÉTRICOS
·
Sólidos geométricos
·
Banco de ejercicios y problemas
·
Evaluación sumativa
PROYECTO4
·
Matemáticamente
·
Autoevaluación
MODULO 5: NÚMEROS INFINITOS
MODULO 5: NÚMEROS INFINITOS
BLOQUE DE RELACIONES Y FUNCIONES : PATRONES DE CRECIMIENTO
LINEAL
·
Patrones de crecimiento lineal
·
Líneas paralelas
·
Líneas perpendiculares
ECUACIONES DE PRIMER GRADO
·
Ecuaciones de primer grado
·
Ecuación
·
Resolución de ecuaciones de primer grado
·
Resolución de problemas con ecuaciones de primer
grado
BLOQUE GEOMÉTRICO: ÁREAS LATERALES DE PRISMAS Y CILINDROS
·
Área lateral de prismas regulares
·
Área lateral de un cilindro
·
Área de sectores circulares
·
Banco de ejercicios y problemas
·
Evaluación sumativa
PROYECTO5
·
Matemáticamente
·
Autoevaluación
MÓDULO 6: ORGANIZAR Y ENTENDER EL MUNDO
MÓDULO 6: ORGANIZAR Y ENTENDER EL MUNDO
BLOQUE DE RELACIONES Y FUNCIONES: INECUACIONES DE PRIMER
GRADO
·
Desigualdades
·
Intervalos
·
Inecuaciones de primer grado
·
Problemas con inecuaciones de primer grado
BLOQUE DE ESTADISTICA Y PROBABILIDAD: MEDIDAS DE TENDENCIA
CENTRAL
·
Banco de ejercicios y problemas
·
Evaluación sumativa
PROYECTO 6
·
Matemáticamente
·
Autoevaluación
Módulo 1
bjetivos
- Leer y escribir números racionales en base a su definición .
- Calcular el área de polígonos regulares e irregulares
·
Representar y analizar datos estadísticos en
diagrama de tallo y hojas
Destrezas con criterio de desempeño.
·
Leer y escribir números racionales en base a su definición
.
·
Representar números fraccionarios en notación decimal
y fraccionaria
·
Ordenar y comparar números fraccionarios
·
Reconocer líneas de simetría en figuras
geométricas
·
Deducir las fórmulas para el cálculo de áreas de
polígonos regulares por la descomposición de triángulos
·
Representar datos estadísticos en diagramas de
tallos y hojas
Módulo 2Objetivos
- Aplicar el teorema de Pitágoras en la resolución de triángulos rectángulos para el cálculo de perímetros y áreas
- Aplicar las operaciones básicas de la radicación
y potenciación en la resolución de problemas con números racionales e
irracionales . o para desarrollar un pensamiento crítico y lógico.
- Utilizar el teorema de Pitágoras en la resolución de triángulos rectángulos
- Resolver operaciones combinadas de adición, sustracción, multiplicación y división exacta con números racionales
- Simplificar expresiones de números racionales con la aplicación de las reglas de potenciación y de radicación
- Resolver operaciones combinadas e adición, sustracción, multiplicación y división exacta con números irracionales
- Representar gráficamente números irracionales con el uso del teorema de Pitágoras
- Ordenar, comparar y utilizar en la recta numérica números irracionales con el uso de la escala adecuada-
CUESTIONARIO PARA EL EXAMEN DEL PRIMER QUIMESTRE
1.- Escriba una V (verdadero) o la F (falso) en el casillero de la derecha de las siguientes afirmaciones, según corresponda.
1.- Un monomio es aquel que tiene un solo termino
| |
2.- Una fracción es propia cuando el numerador es mayor que el denominador
| |
3.- Los términos de la potenciación son: Base, exponente y potencia
| |
4.- El coeficiente del siguiente monomio 6ª2b3c5 3 es igual a 15
| |
5.- Un binomio es aquel que tiene tres términos
| |
6.- La raíz cuadrada de 64 es igual a 8
| |
7.- Una fracción es compleja cuando en el numerador tiene una operación indicada y en el denominador puede tener una fracción
| |
2.- En el paréntesis ubicado a la izquierda de las premisas, escriba las letras que corresponda a la respuesta correcta de entre las opciones de la derecha.
Premisas
|
Respuestas
|
1. ( ) a
2. ( ) m –n
3. ( ) x2 + 2xy + y2
4. ( ) -1
5. ( ) raíz cuadrada 81
6. ( ) ¼
7. ( ) 0.65
|
(A) Binomio
(B) Trinomio
(C) Monomio
(D) Fracción
(E) Numero entero
(F) Raíz
(G) Numero decimal
|
3.- A continuación se presentan cuatro preguntas; razone y escriba la respuesta (solo una) en el espacio en blanco de la derecha, con las opciones que se dan a continuación: NÚMEROS ENTEROS; FRACCIÓN IMPROPIA; NUMERO MIXTO; TRINOMIO.
1.- ¿Cómo se llama el polinomio que tiene tres términos?
| |
2.- Cuando el numerador es mayor que el denominador; ¿Cómo se llama a la fracción?
| |
3.- ¿Cómo se llama al número que tiene un número entero y una fracción?
| |
4.- Cuando existen los siguientes número +3; -3; 0; ¿Cómo se llaman a esos números?
|
ENCIERRE EN UN CÍRCULO LA RESPUESTA CORRECTA:
4.- ¿Cuál es el Orden descendente del siguiente polinomio: 2x4 + 4x7 – 6x + 8x3– 10x2 + 12x5 + 14x6 ?
a) 14x6 + 12x5 - 10x2 + 8x3 - 6x + 4x7 + 2x4
b) – 6x – 10x2 + 8x3 + 2x4 +12x5 + 14x6 + 4x7
c) 4x7 + 14x6 +12x5 + 2x4 + 8x3 – 10x2 - 6x
5.- La factorización es un proceso para obtener:
a) Términos
b) Factores
c) Sumandos
d) Diferencias
6.- El binomio 121x2 – y2 es igual a :
a) ( 11x + y ) ( 11x – y )
b) (11x + y ) (11x +y )
c) (11x – y ) (11x – y)
7.- Términos semejantes son los que tienen igual:
a) Signos
b) Exponentes
c) Parte literal
d) Coeficientes numéricos
PROBLEMAS:
8.- En un día de trabajo (8 horas), un obrero ha hecho 15 cajas ¿Cuántos días de trabajo tardará en hacer 45 cajas?
a) 5 días
b) 6 días
c) 3 días
d) 2 días
9.- La suma de dos artefactos eléctricos es de $ 87,96; si uno de los artefactos eléctricos costo $ 45,60 ¿Cuánto vale el otro?
a) $ 133,56
b) $ 42,36
c) $ 42,30
d) $ 40,36
10.- ¿Cuántos grados tiene el tercer ángulo de un triángulo cuyos otros ángulos son 60 grados y 65 grados?
a) 65 grados
b) 60 grados
c) 55 grados
d) 90 grados
11.- Pedro en un día de trabajo (8 horas), ha hecho 15 sillas ¿Cuántos trabajadores incluyendo a Pedro se necesitara para hacer 90 sillas en un solo día?
b) 6 trabajadores
c) 3 trabajadores
d) 5 trabajadores
12.- La suma de dos artefactos eléctricos es de $187,96; si uno de los artefactos eléctricos costo $ 45,60 ¿Cuánto vale el otro?
a) $ 233,56
b) $ 142,36
c) $ 142,90
d) $ 142.96
13.- En una encuesta realizada con los alumnos de octavo de Educación Básica del Colegio a Distancia “Don Bosco” para saber cuántos hijos se ha obtenido los siguientes resultados: 1; 3; 1; 2; 3; 2; 5; 4; 5; 2; 1; 2; 2; 3; 6; 2; 4 ;3. Complete la tabla con la frecuencia que se repiten los datos y grafique los resultados obtenidos.
Números
|
frecuencia
|
1
| |
2
| |
3
| |
4
| |
5
| |
6
|
(x)
| |||||||||
OPERACIONES CON FRACCIONES
SUMA Y RESTA DE FRACCIONES Heterogeneas
FRACCIONES EQUIVALENTES
SUMA DE FRACCIONES HOMOGENEAS
SUMA Y RESTA DE FRACCIONES HETEROGENEAS
RAIZ DE UNA FRACCIÓN
FRANCIONES CON POTENCIAS
RESTA DE NPUMEROS MIXTOS
BIENVENIDOS A LA TUTORIA DE ALGEBRA
En el siguiente video veremos que es un polinomio, el valor absoluto y valor relativo de un polinomio
Los polinomios, monomios, identificar cual es el coeficiente, la parte literal y el grado, suma y resta de polinomios
Suma de Monomios y Polinomios, reducción de terminos semejantes
En el siguiente video se podrá observar algunos ejercicios para la destrucción de signos de agrupación y términos semejantes.
ADICIÓN Y SUSTRACCIÓN DE POLINOMIOS
MULTIPLICACIÓN Y DIVISIÓN DE POLINOMIOS
MULTIPLICACIÓN DE POLINOMIOS
MULTIPLICACIÓN DE MONOMIOS
DIVISIÓN DE POLINOMIOS
El siguiente es un ejemplo es para sacar el fractor común (primer caso de factoreo)
TERCER CASO: Trinomio Cuadrado Perfecto
Segundo Caso de factoreo: Factor Común en Grupos , Factoricemos un polinomio utilizando los signos de agrupación.
CUARTO CASO: DIFERENCIA DE CUADRADOS
CASO SEPTIMO:
CASO OCTAVO: EL CUBO PERFECTO DE UN BINOMIO
EL CUADRADO DE UN BINOMIO O EL CUADRADO DE UNA SUMA
EL CUADRADO DE UN BINOMIO O EL CUADRADO DE UNA DIFERENCIA
EL PRODUCTO DE LA SUMA POR LA DIFERENCIA DE DOS BINOMIOS
Factorización DEL TRINOMIO CUADRADO PERFECTO
SUMA DE CUBOS PERFECTOS
DIFERENCIA DE CUBOS PERFECTOS
TRINOMIO DE LA FORMA AX^2 +BX+C
ECUASIONES
ECUACIÓN CUADRÁTICA
La utilización de Matrices para resolver los sistemas de ecuaciones por el método de GAUS
LOGARITMOS.
PROPIEDADES DE LOS LOGARITMOS
Matemáticas Noveno año de Educación Básica
CUESTIONARIO PARA EL SEGUNDO QUIMESTRE
y efectue los ejercicios propuestos
--------------------------------------------------------------------------------------------------
IDENTIFICACIÓN DEL TRINOMIO CUADRADO PERFECTO
EJEMPLO 1: Identifique si es un Trinomio Cuadrado Perfecto la siguiente expresión:
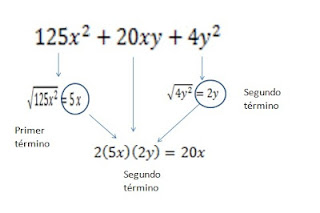
En este caso si es un Trinomio Cuadrado Perfecto la solución es:
(5x+2y)^2
EJERCICIOS PROPUESTOS
1.- Escriba una V (verdadero) o la F (falso) en el casillero de la derecha de las siguientes afirmaciones, según corresponda.
1.- Un monomio es aquel que tiene un solo termino
| |
2.- Una fracción es propia cuando el numerador es mayor que el denominador
| |
3.- Los términos de la potenciación son: Base, exponente y potencia
| |
4.- El coeficiente del siguiente monomio 6b3c5 3 es igual a 18
| |
5.- Un binomio es aquel que tiene tres términos
| |
6.- La raíz cuadrada de 64 es igual a 8
| |
7.- Una fracción es compleja cuando en el numerador tiene una operación indicada y en el denominador puede tener una fracción
| |
2.- En el paréntesis ubicado a la izquierda de las premisas, escriba las letras que corresponda a la respuesta correcta de entre las opciones de la derecha.
Premisas
|
Respuestas
|
1. ( ) a
2. ( ) 3a – 2n
3. ( ) m2 + 2mn + n2
4. ( ) -12
5. ( ) raíz cuadrada 81= 9
6. ( ) ¼
7. ( ) 0.65
|
(A) Binomio
(B) Trinomio
(C) Variable
(D) Fracción
(E) Numero entero
(F) Raíz
(G) Numero decimal
|
3.- A continuación se presentan cuatro preguntas; razone y escriba la respuesta (solo una) en el espacio en blanco de la derecha, con las opciones que se dan a continuación: NÚMEROS ENTEROS; FRACCIÓN IMPROPIA; NUMERO MIXTO; TRINOMIO.
1.- ¿Cómo se llama el polinomio que tiene tres términos?
| |
2.- Cuando el numerador es mayor que el denominador; ¿Cómo se llama a la fracción?
| |
3.- ¿Cómo se llama al número que tiene un número entero y una fracción?
| |
4.- Cuando existen los siguientes número +3; -3; 0; ¿Cómo se llaman a esos números?
|
ENCIERRE EN UN CÍRCULO LA RESPUESTA CORRECTA:
4.- Ordene el siguiente polinomio: 2x4 + 4x7 – 6x + 8x3– 10x2 + 12x5 + 14x6
a) 14x6 + 12x5 - 10x2 + 8x3 - 6x + 4x7 + 2x4
b) – 6x – 10x2 + 8x3 + 2x4 +12x5 + 14x6 + 4x7
c) 4x7 + 14x6 +12x5 + 2x4 + 8x3 – 10x2 - 6x
5.- La factorización es un proceso para obtener:
a) Términos
b) Factores
c) Sumandos
d) Diferencias
6.- El binomio 121x2 – y2 es igual a :
a) ( 11x + y ) ( 11x – y )
b) (11x + y ) (11x +y )
c) (11x – y ) (11x – y)
7.- Términos semejantes son los que tienen igual:
a) Signos
b) Exponentes
c) Parte literal
d) Coeficientes numéricos
PROBLEMAS:
8.- En un día de trabajo (8 horas), un obrero ha hecho 15 cajas ¿Cuántos días de trabajo tardará en hacer 45 cajas?
a) 5 días
b) 6 días
c) 3 días
d) 2 días
9.- La suma de dos artefactos eléctricos es de $ 87,96; si uno de los artefactos eléctricos costo $ 45,60 ¿Cuánto vale el otro?
a) $ 133,56
b) $ 42,36
c) $ 42,30
d) $ 40,36
10.- ¿Cuántos grados tiene el tercer ángulo de un triángulo cuyos otros ángulos son 60 grados y 65 grados?
a) 65 grados
b) 60 grados
c) 55 grados
d) 90 grados
11.- Pedro en un día de trabajo (8 horas), ha hecho 15 sillas ¿Cuántos trabajadores incluyendo a Pedro se necesitara para hacer 90 sillas en un solo día?
b) 6 trabajadores
c) 3 trabajadores
d) 5 trabajadores
12.- La suma de dos artefactos eléctricos es de $187,96; si uno de los artefactos eléctricos costo $ 45,60 ¿Cuánto vale el otro?
a) $ 233,56
b) $ 142,36
c) $ 142,90
d) $ 142.96
1.- Escriba una V (verdadero) o la F (falso) en el casillero de la derecha de las siguientes afirmaciones, según corresponda.
1.- 3(4x + 1 ) = 3(4x) + 3(1) = 12x + 3 Propiedad distributiva de la multiplicación
| |
2.-
| |
3.- Los términos de la potenciación son: Base, exponente y potencia
| |
4.- El coeficiente del siguiente monomio 6b3c5 3 es igual a 18
| |
5.- 7a – 15 = 2a Ecuación de segundo grado con una incógnita
|
2.- En el paréntesis ubicado a la izquierda de las premisas, escriba las letras que corresponda a la respuesta correcta de entre las opciones de la derecha.
Premisas
|
Respuestas
|
1. ( ) a
2. ( ) m –n = 3
3. ( ) 2 , 4 , 6 , 8 , 10……
4. ( ) 3x + 2 < 5
5. ( )
6. ( )
7. ( ) 33 = 27
|
(A) Ecuación
(B) Sucesiones
(C) variable
(D) Formula
(E) Inecuación
(F) Raíz Cuadrada
(G) Potencia
|
3.- Una con una línea lo correcto:
a+ b = 2
2a - b = 5
|
Teorema de Pitágoras
|
c =
|
Sistema de ecuaciones de 2 X 2
|
Cuadriláteros
| |
Función trigonométrica
|
ENCIERRE EN UN OVALO LA RESPUESTA CORRECTA:
4.- Resuelva la ecuación 2 + 3x = 5x - 6
a) X = - 4
b) X = 4
c) X = 2
5.- Carlos le dice a un compañero: El doble de mi edad más 3 es igual al triple de mi edad menos 13, ¿Qué edad tiene Carlos?
En este caso la ecuación que se plantea es: 2x + 3 = 3x -13
a) 15 años
b) 20 años
c) 16 años
d) 18 años
PROBLEMAS:
6.- La suma de los ángulos de un triángulo cualquiera es siempre 180°. Sabiendo que un triángulo rectángulo es aquel que tiene un ángulo de 90°. Por tanto, la suma de los dos ángulos agudos de un triángulo rectángulo es: 180o - 90o = 90°. Completa las líneas de puntos siguientes:
• Si un ángulo agudo de un triángulo rectángulo mide 60°, el otro mide ……........
• Si un ángulo agudo de un triángulo rectángulo mide 30°, el otro mide.....................
• Si un ángulo agudo de un triángulo rectángulo mide 45°, el otro mide.....................
GRAFIQUE
7.- Dado los siguientes datos represente gráficamente la ecuación X + Y = 7
X
|
Y = 7 - X
|
1
|
6
|
2
|
5
|
5
|
2
|


















